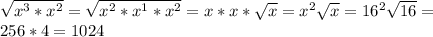
V(x^3*x^2)=x^2.5
x^2.5=16^2.5=1024
Объяснение:
Чтобы записать данные нам выражения в виде многочлена, мы должны воспользоваться формулами сокращенного умножения.
Пример №1.
(3c - xy)^2
Данная формула называется квадратом разности.
(a - b)^2 = a^2 - 2ab + b^2 - вот вид данной формулы.
Теперь идем по порядку:
Квадрат первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа.
Получаем:
9c^2 - 6cxy + xy^2 - окончательный результат.
Пример №2.
(3 + 5a)(3 - 5a)
Данная формула называется разностью квадратов.
Для того, чтобы решить этот пример, мы берем скобку со знаком минус, и возводим оба числа(стоящие в скобке) в квадрат.
То есть:
3^2 - 5a^2
Или же 9 - 25a^2
Задача решена.
Если есть вопросы - задавай.
1.1) arcsin(-1) + arccos0 = π + (π/2) = 3π/2
Пусть arcsin(-1) = α, тогда cosα = -1, значит α = π
Пусть arccos0 = β, тогда cosβ = 0, значит β = (π/2)
2) arctg + arctg(- √3) = π/4 + (-π/3) = 1
2. x=±arccosa+2πk,k∈Z .
3.tg(2x) = 2·tg(x)/(1 - tg²(x))
4.cos 5x-cos 7x=0
-2sin 6x*sin (-x)=0(-2 на синус полусуммы углов умножить на синус полуразности углов)
sin 6x=0 или sin x=0
6x=pn, x=pn/6 или x=pn
x=pn/6
5. sin (3x) =1
3х= π/2+2πn
x= π/6 + (2πn)/3
7. sin(3x)-sin(x)=0
2*sin((3x-x)/2)*cos((3x+x)/2)=0
2sin(x)*cos(2x)=0
1) sin(x)=0
x=π*n
2) cos(2x)=0
2x=(pi/2)+pi*n
x=(pi/4)+pi*n/2