![1)\sqrt[5]{0,00032}= \sqrt[5]{(0,2)^{5}}=0,2\\\\2)\sqrt[4]{\frac{16}{625}} = \sqrt[4]{(\frac{2}{5})^{4}}= \frac{2}{5}=0,4](/tpl/images/0945/7260/13ce2.png)
![\sqrt[5]{0,00032}=\sqrt[5]{32}*\sqrt[5]{0,00001}=2*0,1=0,2](/tpl/images/0945/7260/dcde8.png)
![\sqrt[4] {\frac{16}{625}}=\sqrt[4] {\frac{2^4}{5^4}}=\frac{2}{5}](/tpl/images/0945/7260/18074.png)
а) При сравнении десятичных дробей в первую очередь нужно сравнивать целые части (они расположены слева от запятой). Так как целые части равны, то сравниваем дробные части
0.382 < 3*2 ⇔ 0.382 < 0.392 ⇒ потому что 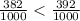
Следовательно, 5.382 < 5.392
б) Аналогично, целые части равны, тогда сравниваем дробные части
0.* < 0.2 ⇔ 0.1 < 0.2 так как 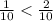
Следовательно, 31.1 < 31.2
в) У первого числа символов после запятой не совпадает со вторым числом, тогда к дроби наименьшим количеством символов приписываем нули и сравним получившиеся числа дробных частей
0.10 > 0.*1 ⇔ 0.10 > 0.01 так как 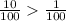
Следовательно, 7.1 > 7.01
г) Аналогично с примера в), рассуждения такие же:
0.010 < 0.*08 ⇔ 0.010 < 0.108 потому что 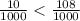
Следовательно, 7.01 < 7.108
Объяснение:
Сначало надо извлечь кубический корень из 343 это будет 7, следует что куб 7x7x7. Дальше смотрим у каких частей на одной стороне куба одна или 0 окрашенных граней, их 25, это внутренний квадрат стороны.
Дальше нам надо понять у каких кубиков 0 окрашенных граней, это все кубики которые находятся внутри большого куба. Нам надо узнать сколько кубиков 0 окрашенных граней, так как всего 25 окрашенных с 1 граней, надо 25*5 потому что внутри всего 5 рядов.
Получается 125 и нам осталось прибавить кубики которые с 1 окрашенной граней их 25*6, 6 потому что у куба 6 сторон.
Получается 125 + 150 = 275, 343-275=68.
ответ: 68 кубиков.