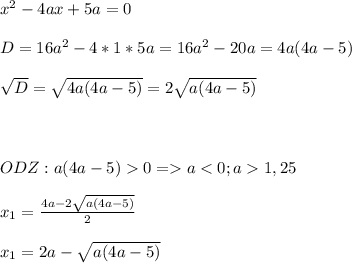
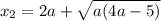
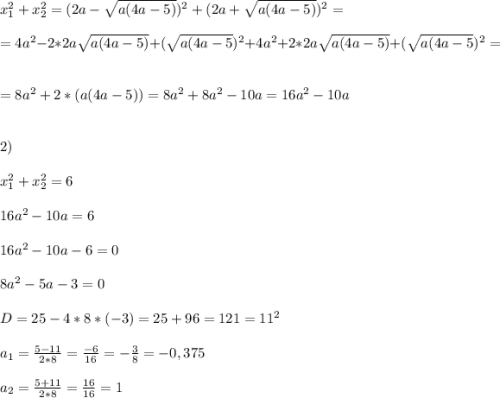
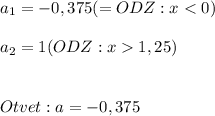
Пусть y = uv, тогда y' = u'v + uv':
Решим левый интеграл:
cosx = \frac{1-t^2}{1+t^2} => dx = \frac{2}{1+t^2}dt\\ \int \frac{2(1+t^2)}{(1+t^2)(1-t^2)} dt = \int \frac{2}{(1-t)(1+t)}dt = \int ( \frac{1}{1-t} + \frac{1}{1+t})dt = ln(1-t)+ln( 1+t) = ln|1-t^2| = ln|1-tg^2\frac{x}{2}| \\" class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=%5Cint%20%5Cfrac%7Bdx%7D%7Bcosx%7D%3B%5C%5C%20tg%5Cfrac%7Bx%7D%7B2%7D%3Dt%20%3D%3E%20cosx%20%3D%20%5Cfrac%7B1-t%5E2%7D%7B1%2Bt%5E2%7D%20%3D%3E%20dx%20%3D%20%5Cfrac%7B2%7D%7B1%2Bt%5E2%7Ddt%5C%5C%20%20%5Cint%20%5Cfrac%7B2%281%2Bt%5E2%29%7D%7B%281%2Bt%5E2%29%281-t%5E2%29%7D%20dt%20%3D%20%5Cint%20%5Cfrac%7B2%7D%7B%281-t%29%281%2Bt%29%7Ddt%20%3D%20%5Cint%20%28%20%5Cfrac%7B1%7D%7B1-t%7D%20%2B%20%5Cfrac%7B1%7D%7B1%2Bt%7D%29dt%20%3D%20ln%281-t%29%2Bln%28%201%2Bt%29%20%3D%20ln%7C1-t%5E2%7C%20%3D%20ln%7C1-tg%5E2%5Cfrac%7Bx%7D%7B2%7D%7C%20%20%5C%5C" title="\int \frac{dx}{cosx};\\ tg\frac{x}{2}=t => cosx = \frac{1-t^2}{1+t^2} => dx = \frac{2}{1+t^2}dt\\ \int \frac{2(1+t^2)}{(1+t^2)(1-t^2)} dt = \int \frac{2}{(1-t)(1+t)}dt = \int ( \frac{1}{1-t} + \frac{1}{1+t})dt = ln(1-t)+ln( 1+t) = ln|1-t^2| = ln|1-tg^2\frac{x}{2}| \\">
Возвращаемся к исходному:
1) Орг. момент.
2) Актуализация опорных знаний.
Определение. Линейным уравнением с двумя переменными называется уравнение вида
mx + ny = k, где m, n, k – числа, x, y – переменные.
Пример: 5x+2y=10
Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.
1. 5x+2y=12 (2)y = -2.5x+6
Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.
Пусть x = 2, y = -2.5•2+6 = 1
x = 4, y = -2.5•4+6 =- 4
Пары чисел (2;1); (4;-4) – решения уравнения (1).
Данное уравнение имеет бесконечно много решений.
3) Историческая справка
Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.
В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.
Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.
4) Изучение нового материала.
Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y Z k0
Утверждение 1.
Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Пример: 34x – 17y = 3.
НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет.
Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно Утверждение 2.
Если m и n уравнения (1) взаимно числа, то это уравнение имеет по крайней мере одно решение.
Утверждение 3.
Если коэффициенты m и n уравнения (1) являются взаимно числами, то это уравнение имеет бесконечно много решений:
где (; ) – какое-либо решение уравнения (1), t Z
Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)
m, n, x, y Z
Утверждение 4.
Если m и n – взаимно числа, то всякое решение уравнения (2) имеет вид
5) Домашнее задание. Решить уравнение в целых числах:
9x – 18y = 5
x + y= xy
Несколько детей собирали яблоки. Каждый мальчик собрал по 21 кг, а девочка по 15 кг. Всего они собрали 174 кг. Сколько мальчиков и сколько девочек собирали яблоки?
Замечание. На данном уроке не представлены примеры решения уравнений в целых числах. Поэтому домашнее задание дети решают исходя из утверждения 1 и подбором.
Урок 2.
1) Организационный момент
2) Проверка домашнего задания
1) 9x – 18y = 5
НОД (9;18)=9
5 не делится нацело на 9, в целых числах решений нет.
2) x + y= xy
Методом подбора можно найти решение
ответ: (0;0), (2;2)
Два действительных корня, значит x₁≠x₂ и 16a²-20a>0;
4a²-5a>0;
a(4a-5)>0;
нули функции 0; 4a>5; a>1,25;
+ - +
___0___1,25___
-∞<a; a>1,25;
сумма квадратов которых равна 6: x₁²+x₂²=6; (1)
По теореме Виетта:
x₁+x₂=-p=4a;(2)
x₁x₂=q=5a;(3)
Эти три уравнения составляют систему.
сложим (2) и дважды (3).
Возведем в квадрат (2)
(x₁+x₂)²=(4a)²;
x₁²+2x₁x₂+x₂²=16a²; отнимем дважды (3);
x₁²+2x₁x₂+x₂²-2x₁x₂=16a²-2*5a;
x₁²+x₂²=16a²-10a; подставим вместо левой части уравнение (1).
6=16a²-10a; разделим на 2;
8a²-5a-3=0;
D=25+4*8*3=121;
a₁=(5+11)/16=1;∅, по ОДЗ a.
a₂=(5-11)/16=-3/8;
Проверка:
x²+1,5x-1,875=0;
8x²+12x-15=0;
D=144+4*8*15=624=16*39;
x₁=(-12+4√39)/16=-0,75+0,25√39;
x₂=(-12-4√39)/16=-0,75-0,25√39;
Подставим в формулы (2) и (3):
x₁+x₂=4a; -0,75+0,25√39-0,75-0,25√39=-4*3/8; -1,5=-1,5;
x₁x₂=5a; (-0,75+0,25√39)(-0,75-0,25√39)=-5*3/8;
0,75²-(0,25√39)²=-15/8;
0,5625-0,0625*39=-1,875;
-1,875=-1,875;
ответ: a=-3/8;