у=2(х-2)*-1
у=(2х-4)*-1
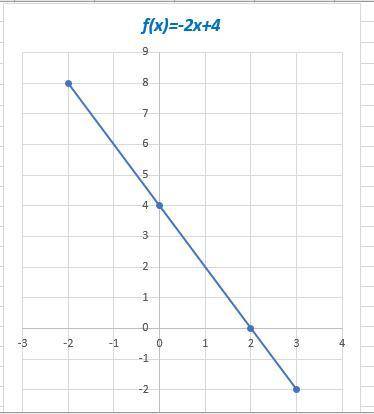
у=-2х+4
f(x)=-2x+4 - линейная функция, график - прямая
Область определения D(f) x∈R (множество всех действительных чисел)
Множество значений E(f) y∈R я
Нет максимума и минимума, непериодическая (непрерывна), ни четная, ни нечетная.
k=-2 => k<0 - функция убывающая, график образует тупой угол с положительным направлением оси 0Х.
График строится по 2-м точкам.
Можно найти точки пересечения графика с осями координат и построить график по ним.
Пересечение с осью 0Х: х=0 => y=-2*0+4=4 (0;4)
Пересечение с осью 0У: y=0 => х=-4/-2=2 (2;0)
E(y) -- это область значений функции.
В данном примере проще оценить выражение(нужно понять, когда функция принимает минимальное и максимальное значение):
Меняется в этой функции только sin. sin(2-3x) принимает значения от -1 до 1, то есть минимальное значение у функции будет при sin(2-3x) = 1, а максимальное при sin(2-3x) = -1:
1. 6 - 4sin(2-3x) = 6 - 4*(-1) = 10
2. 6 - 4sin(2-3x) = 6 - 4*1 = 2
E(y) = [2; 10]
Есть более универсальный Оценить область значений можно с производной.
С её можно найти точки максимума и минимума, а после и сами значения функции в этих точках.
А если функция претерпевает разрыв (гипербола например), то производная найти "подозрительную точку". Понять, стремиться ли в этой точке функция к бесконечности можно с пределов (но они в школе изучаются в старших классах обычно). Поэтому опираются чаще на свойства функции (на примере гиперболы -- всегда ветви уходят вверх, к бесконечности) или стараются оценить подставляя некоторые значения х(но подставлять значения наугад -- не самый эффективный метод)
(x²-5x-4)²-3(x³-5x²-4x)+2x²=0
Учтём, что (x³-5x²-4x) = х( х² -5х -4)
Теперь введём новую переменную х² -5х -4 = t
Наше уравнение примет вид:
t² -3xt +2x² = 0
решаем относительно переменной t
D = b² -4ac = 9x² - 8x² = x²
t = (3x +- |x|)/2
1) при х ≥ 0 2) при х < 0
t₁ = 2x и t₂= x t₃ = x и t₄ = 2x
Теперь возвращаемся к нашей подстановке.
x² -5x -4 = 2x или x² -5x -4 = x
x² -7x -4 = 0 x² -6x -4 = 0
D = 49+16 = 65 x₃₎₄ =3 +-√13
x₁₎₂ = (7+-√65)/2