![y=tgx\\\\y'=\lim\limits _{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim\limits _{\Gelta x \to 0}\frac{tg(x+\Delta x)-tgx}{\Delta x}=\lim\limits _{\Delta x \to 0}\frac{sin(x+\Delta x-x)}{cos(x+\Delta x)\cdot cosx\cdot \Delta x}=\\\\=\lim\limits _{\Delta x \to 0}\frac{sin\Delta x}{\frac{1}{2}\cdot (\, cos(x+\Delta x+x)+cos(x+\Delta x-x)\, )\cdot \Delta x}=\lim\limits _{\Delta x \to 0}\frac{2\Delta x}{\Delta x\cdot (\, cos(2x+\Delta x)+cos\Delta x\, )}=\\\\=\lim\limits_{\Delta x \to 0}\frac{2}{cos(2x+\Delta x)+cos\Delta x}=\Big [\, \Delta x\to 0\, \Big ]=\frac{2}{cos2x+cos0}=\frac{2}{cos2x+1}=\\\\=\frac{2}{2cos^2x}=\frac{1}{cos^2x}\\\\(tgx)'=\frac{1}{cos^2x}](/tpl/images/0947/9154/8dfda.png)
У числа 6 четыре делителя. 1, 2, 3, 6. Для того, чтобы число было взаимнопросто с 6, необходимо и достаточно, что бы оно не делилось на 2 и 3 (Так как если оно делится на 6, то оно делится и на 2 и 3)
Каждое второе число делится на 2, каждое третье - на 3. Среди них, каждое шестое делится и на 2 и на 3.
Количство чисел взаимнопростых с 6 до натурального числа N, есть:
![N - [\frac{N}{2}] - [\frac{N}{3}] + [\frac{N}{6}]](/tpl/images/0155/6965/63f6c.png)
N = 30
30 - 15 - 10 + 5 = 10
Это числа 1, 5, 7, 11, 13, 17, 19, 23, 25, 29
---------------------------------------------------------------------
![[x]](/tpl/images/0155/6965/6e538.png) - это целая часть x. Например [2.44] = 2, [0.1] = 0
- это целая часть x. Например [2.44] = 2, [0.1] = 0
Выражение: (18*a^4*b+60*a^3*b^2+48*a^2*b^3):6*a^2*b-(a+b)*(3*a+7*b)
ответ: 3*a^6*b^2+10*a^5*b^3+8*a^4*b^4-a^2*3-10*a*b-b^2*7
Решаем по действиям:
1. (18*a^4*b+60*a^3*b^2+48*a^2*b^3):6=18*a^4*b/6+60*a^3*b^2/6+48*a^2*b^3/6
2. 18/6=3
18|6_ _
1_8_|3
0
3. 60/6=10
60|6_ _
6_ |10
0
4. 48/6=8
48|6_ _
4_8_|8
0
5. (3*a^4*b+10*a^3*b^2+8*a^2*b^3)*a^2=3*a^6*b+10*a^5*b^2+8*a^4*b^3
(3*a^4*b+10*a^3*b^2+8*a^2*b^3)*a^2=3*a^4*b*a^2+10*a^3*b^2*a^2+8*a^2*b^3*a^2
5.1. a^4*a^2=a^6
a^4*a^2=a^(4+2)
5.1.1. 4+2=6
+4
_2_
6
5.2. a^3*a^2=a^5
a^3*a^2=a^(3+2)
5.2.1. 3+2=5
+3
_2_
5
5.3. a^2*a^2=a^4
a^2*a^2=a^(2+2)
5.3.1. 2+2=4
+2
_2_
4
6. (3*a^6*b+10*a^5*b^2+8*a^4*b^3)*b=3*a^6*b^2+10*a^5*b^3+8*a^4*b^4
(3*a^6*b+10*a^5*b^2+8*a^4*b^3)*b=3*a^6*b*b+10*a^5*b^2*b+8*a^4*b^3*b
6.1. b*b=b^2
b*b=b^(1+1)
6.1.1. 1+1=2
+1
_1_
2
6.2. b^2*b=b^3
b^2*b=b^(2+1)
6.2.1. 2+1=3
+2
_1_
3
6.3. b^3*b=b^4
b^3*b=b^(3+1)
6.3.1. 3+1=4
+3
_1_
4
7. (a+b)*(3*a+7*b)=a^2*3+10*a*b+b^2*7
(a+b)*(3*a+7*b)=a*3*a+a*7*b+b*3*a+b*7*b
7.1. a*a=a^2
a*a=a^(1+1)
7.1.1. 1+1=2
+1
_1_
2
7.2. a*7*b+b*3*a=10*a*b
7.3. b*b=b^2
b*b=b^(1+1)
7.3.1. 1+1=2
+1
_1_
2
8. 3*a^6*b^2+10*a^5*b^3+8*a^4*b^4-(a^2*3+10*a*b+b^2*7)=3*a^6*b^2+10*a^5*b^3+8*a^4*b^4-a^2*3-10*a*b-b^2*7
Решаем по шагам:
1. (18*a^4*b/6+60*a^3*b^2/6+48*a^2*b^3/6)*a^2*b-(a+b)*(3*a+7*b)
1.1. (18*a^4*b+60*a^3*b^2+48*a^2*b^3):6=18*a^4*b/6+60*a^3*b^2/6+48*a^2*b^3/6
2. (3*a^4*b+60*a^3*b^2/6+48*a^2*b^3/6)*a^2*b-(a+b)*(3*a+7*b)
2.1. 18/6=3
18|6_ _
1_8_|3
0
3. (3*a^4*b+10*a^3*b^2+48*a^2*b^3/6)*a^2*b-(a+b)*(3*a+7*b)
3.1. 60/6=10
60|6_ _
6_ |10
0
4. (3*a^4*b+10*a^3*b^2+8*a^2*b^3)*a^2*b-(a+b)*(3*a+7*b)
4.1. 48/6=8
48|6_ _
4_8_|8
0
5. (3*a^6*b+10*a^5*b^2+8*a^4*b^3)*b-(a+b)*(3*a+7*b)
5.1. (3*a^4*b+10*a^3*b^2+8*a^2*b^3)*a^2=3*a^6*b+10*a^5*b^2+8*a^4*b^3
(3*a^4*b+10*a^3*b^2+8*a^2*b^3)*a^2=3*a^4*b*a^2+10*a^3*b^2*a^2+8*a^2*b^3*a^2
5.1.1. a^4*a^2=a^6
a^4*a^2=a^(4+2)
5.1.1.1. 4+2=6
+4
_2_
6
5.1.2. a^3*a^2=a^5
a^3*a^2=a^(3+2)
5.1.2.1. 3+2=5
+3
_2_
5
5.1.3. a^2*a^2=a^4
a^2*a^2=a^(2+2)
5.1.3.1. 2+2=4
+2
_2_
4
6. 3*a^6*b^2+10*a^5*b^3+8*a^4*b^4-(a+b)*(3*a+7*b)
6.1. (3*a^6*b+10*a^5*b^2+8*a^4*b^3)*b=3*a^6*b^2+10*a^5*b^3+8*a^4*b^4
(3*a^6*b+10*a^5*b^2+8*a^4*b^3)*b=3*a^6*b*b+10*a^5*b^2*b+8*a^4*b^3*b
6.1.1. b*b=b^2
b*b=b^(1+1)
6.1.1.1. 1+1=2
+1
_1_
2
6.1.2. b^2*b=b^3
b^2*b=b^(2+1)
6.1.2.1. 2+1=3
+2
_1_
3
6.1.3. b^3*b=b^4
b^3*b=b^(3+1)
6.1.3.1. 3+1=4
+3
_1_
4
7. 3*a^6*b^2+10*a^5*b^3+8*a^4*b^4-(a^2*3+10*a*b+b^2*7)
7.1. (a+b)*(3*a+7*b)=a^2*3+10*a*b+b^2*7
(a+b)*(3*a+7*b)=a*3*a+a*7*b+b*3*a+b*7*b
7.1.1. a*a=a^2
a*a=a^(1+1)
7.1.1.1. 1+1=2
+1
_1_
2
7.1.2. a*7*b+b*3*a=10*a*b
7.1.3. b*b=b^2
b*b=b^(1+1)
7.1.3.1. 1+1=2
+1
_1_
2
8. 3*a^6*b^2+10*a^5*b^3+8*a^4*b^4-a^2*3-10*a*b-b^2*7
8.1. 3*a^6*b^2+10*a^5*b^3+8*a^4*b^4-(a^2*3+10*a*b+b^2*7)=3*a^6*b^2+10*a^5*b^3+8*a^4*b^4-a^2*3-10*a*b-b^2*7
По определению, производная есть предел отношения приращения функции к вызвавшему его приращению аргумента, при условии стремления этого приращения аргумента к нулю.
Для функции тангенса имеем:
Преобразуем разность тангенсов по формуле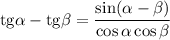 :
:
Рассмотрим предел произведения как произведение пределов:
Значение первого предела-сомножителя равно 1 (первый замечательный предел). Вычисляя второй предел-сомножитель, получим итоговый результат:
Таким образом: