1). x=(-14)/(-2)=7. ответ: x=7. 2). 3x+5x=3-2, 8x=1, x=1/8. ответ: x=1/8. 3). 9-8x+11=12, -8x=12-11-9, -8x= -8, x=(-8)/(-8)=1. ответ: x=1. 4). 2a+6+3a-9=1, 2a+3a=1+9-6, 5a=4, a=4/5. ответ: a=4/5.
 км/ч - скорость пассажирского поезда, тогда
км/ч - скорость пассажирского поезда, тогда 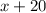 км/ч - скорость скорого поезда. За 3 часа пассажирский поезд пройдет путь в
км/ч - скорость скорого поезда. За 3 часа пассажирский поезд пройдет путь в 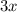 км. Значит и пассажирский и скорый поезд стартуют одновременно с отметки
км. Значит и пассажирский и скорый поезд стартуют одновременно с отметки 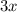 км и пройдут
км и пройдут  км до следующей станции. Отсюда следует, что время движения пассажирского поезда
км до следующей станции. Отсюда следует, что время движения пассажирского поезда 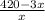 ч, а скорого -
ч, а скорого - 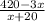 ч. Зная, что скорый поезд прибыл на станцию на 1 час раньше пассажирского, составим уравнение:
ч. Зная, что скорый поезд прибыл на станцию на 1 час раньше пассажирского, составим уравнение: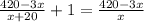
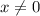 , смело умножим обе части уравнения на
, смело умножим обе части уравнения на 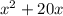 .
.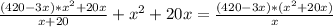
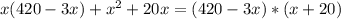
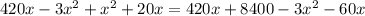
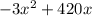
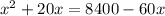
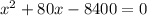
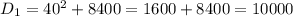
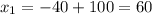
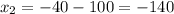
х = (-14) ÷ (-2)
х = 7.
ответ : х = 7.
2. 3х + 2 = 3 - 5х
3х + 5х = 3 - 2
8х = 1
х = 1 ÷ 8
х = 0,125.
ответ : х = 0,125.
3. 9 - ( 8х - 11 ) = 12
9 - 8х + 11 = 12
-8х = 12 - 9 - 11
-8х = -8
х = (-8) ÷ (-8)
х = 1.
ответ : х = 1.
4. 2 ( а + 3 ) + 3 ( а - 3 ) = 1
2а + 6 + 3а - 9 = 1
2а + 3а = 1 - 6 + 9
5а = 4
а = 4 ÷ 5
а = 0,8.
ответ : а = 0,8.
Удачи