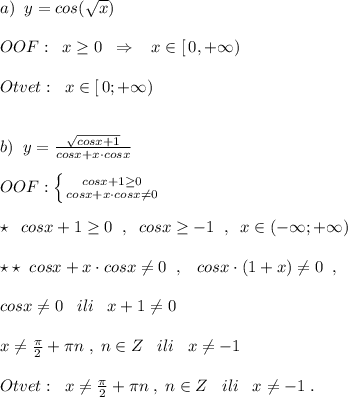
 b)[tex]y = \frac{ \sqrt{ \cos(x" />
b)[tex]y = \frac{ \sqrt{ \cos(x" />
Объяснение:
На фото
в I координатной четверти С(5,5; 5,5)
во II координатной четверти В(-5,5; 5,5)
в III координатной четверти Д(5,5; -5,5)
в IV координатной четверти А(-5,5; -5,5)
Объяснение:
по условию квадрат расположен так, что его стороны параллельны осям координат и делят каждую из его сторон пополам;
так как каждая из сторон равна 11, то от осей его вершины отстают на 11 : 2 = 5,5 ед отрезков. Получаем вершины квадрата, начиная с левой нижней:
А(-5,5; -5,5) в IV координатной четверти
В(-5,5; 5,5) во II координатной четверти
С(5,5; 5,5) в I координатной четверти
Д(5,5; -5,5) в III координатной четверти
давайте решим два линейных неравенства 1) 5(3x - 5) > 3(1 + 5x) - 10, 2) 5(4x - 1) < 5(2x + 3) + 2x используя тождественные преобразования.
давайте начнем с открытия скобок в обеих частях неравенства:
1) 5(3x - 5) > 3(1 + 5x) - 10;
5 * 3x - 5 * 5 > 3 * 1 + 3 * 5x - 10;
15x - 25 > 3 + 15x - 10;
группируем подобные в разных частях неравенства:
15x - 15x > 3 - 10 + 25;
x(15 - 15) > 18;
0 > 18.
неравенство не верное, значит нет решения неравенства.
2) 5(4x - 1) < 5(2x + 3) + 2x;
20x - 5 < 10x + 15 + 2x;
20x - 10x - 2x < 15 + 5;
8x < 20;
x < 20 : 8;
x < 2.5.
x принадлежит промежутку (- бесконечность; 2,5).