Интересное задание. Не такое легкое, как может показаться. И уж не на
Пусть х - число булочек с повидлом, у - число булочек с маком. Тогда, Исходя из первого предложения получаем нестрогое неравенство
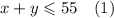
Теперь из второго предложения можно сказать, что
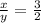 , то есть 2x=3y или x=1,5y. Подставим в (1) неравенство
, то есть 2x=3y или x=1,5y. Подставим в (1) неравенство
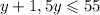
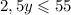
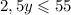
Разделим на 5 обе части неравенства
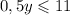
Теперь умножим на 2 обе части неравенства
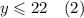
То есть булочек с маком было не больше 22.
Если умножить обе части неравенства (2) на 1,5, то получим
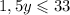
Заметим, что x=1,5, то есть
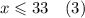
Можно было бы предположить х=33, у=22. Тем более их сумма равна 55, но есть третье и четвертое предложение, которые опровергают эту версию.
После продажи булочек стало на 4 меньше, следовательно их число не превышает (55-4)=51. Не более 51 булочки осталось на витрине. Мы не знаем сколько каждого вида было продано, теперь нам придется вводить новые переменные, чтобы решить теперь это неравенство как предыдущее. Пусть u - булочки с повидлом. v - булочки с маком. Тогда получаем новое неравенство
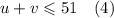
Условие из четвертого предложения должно говорить
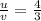
3u=4v
Разделим обе части на 4, получим
v=0,75u
Подставим в (4) значение v через u.
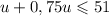
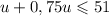
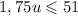
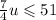
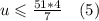
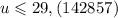
Так как булочек может быть лишь целое число, то
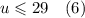
Теперь умножим обе части (5) на 0,75. Получим
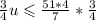
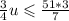
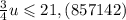
Заметим, что в левой части неравенства стоит v. Так как v - может быть только целым число, то
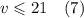
Остальное не умещается, смотри в прикрепленном файле
ответ: 60 см
Объяснение:
Пусть гипотенуза прямоугольного треугольника х см, ( х>16) тогда согласно условия задачи, один из катетов равен (х-16) см, а другой катет равен (х-2) см.
По Теореме Пифагора следует:
х²=(х-16)²+(х-2)²
х²=х²-32х+256+х²-4х+4
х²-х²+32х-256-х²+4х-4=0
-х²+36х-260=0 (* на (-1)
х²-36х+260=0
х1,2=(36+-D)/2
D=√(36²-4*1*260)=√(1296-1040)=√256=16
х1,2=(36±16)/2
х1=(36+16)/2
х1=26
х2=(36-16)/2=10 - не подходит, так как х>16
Тогда катеты равны 26-16=10 26-2=24
Периметр это есть сумма всех трех сторон:
Р=26+10+24=60 см
ответ : 60 см