Площадь прямоугольника равна длине, умноженной на ширину .
(a-b)(a+b)=S₃+S₄ , прямоугольник заштрихован зелёными линиями , состоящий из суммы двух прямоугольников S₃ и S₄ .
Площадь квадрата, обведённого синим контуром равна a²=S₁+S₂+S₃ .
Площадь квадрата, обведённого жёлтым контуром равна b²=S₁ .
Если от площади квадрата а² вычесть площадь квадрата b², то получим а²-b²=(S₁+S₂+S₃)-S₁=S₂+S₃ .
Получившаяся область заштрихована красными линиями. Она состоит из суммы двух прямоугольников S₂ и S₃ , площади которых равны S₂=b(a-b)=ab-b² , S₃=a(a-b)=a²-ab .
S₂+S₃=ab-b²+a²-ab=a²-b²
S₃+S₄=a(a-b)+b(a-b)=S₃+S₂ , S₃+S₄=a²-b² .
Геометрически площадь области, заштрихованной зелёной штриховкой, равна площади области, заштрихованной красной штриховкой: S₂+S₃=S₃+S₄ .
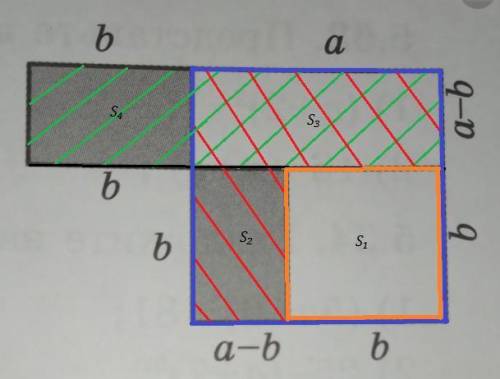
См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
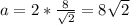 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
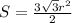 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)

и будет на расстоянии 480-157,5 = 322,5 км от города Б