Question

X^4 +(a^2-a+1)*x^2-a^3-a=0. определите значение параметра а, при которых: 1) уравнение имеет единственный корень; 2) имеет два различных корня; 3) не имеет корней. x^2=t, t=> 0

Answer 1

Итак, ситуация номер 1 - имеется единственное решение:

Если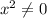 $x^2\neq 0$, то имеется либо 2 и более корней, либо их вообще нет.

Мы знаем, что x=0, тогда

$-a^3-a=0\\a(a^2+1)=0\\a=0$

Решения для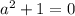 $a^2+1=0$ просто откидываем, комплексные числа нам неинтересны.

Первая ситуация разобрана, но проверку стоит провести:

$x^2=t\\t^2+t=0\\t=0$

Второе решение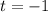 $t=-1$ не подходит, т.к.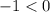 $-1$

$t=0 \Rightarrow x^2=0 \Rightarrow x=0$

Проверка выполнена, имеется единственное решение при a=0

Вторая ситуация:

Необходимо 2 корня, значит значение t будет единственным!

$t^2+(a^2-a+1)t-a^3-a=0\\D=0 \\\therefore (a^2-a+1)^2-4(-a^3-a)=0\\a^4+a^2+1-2a^3+2a^2-2a+4a^3+4a=0\\a^4+2a^3+3a^2+2a+1=0$

Данное уравнение не имеет решений, и при любом значении a D>0 (D по t).

Т.е. мы не имеем решений для второй ситуации.

Третья ситуация:

Т.к. D>0, то и в третьей ситуации удовлетворяющих значений a просто нет.