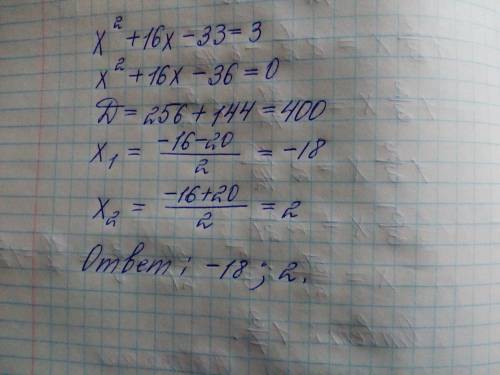
В решении.
Объяснение:
Постройте графики функций y= -3/x и y=x+4 Укажите координаты точек пересечения этих графиков.
График y= -3/x гипербола. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -5 -4 -3 -2 -1,5 -1 -0,5 1 1,5 2 3 4 5
у 0,6 0,75 1 1,5 2 3 6 -3 -2 -1,5 -1 -0,75 -0,6
y=x+4. Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у 3 4 5
Координаты точек пересечения гиперболы и прямой (-1; 3) (-3; 1).
Точки пересечения находятся во второй четверти.
Объяснение:
1)Построить график функции у= -х²-2х+3.
График - парабола со смещённым центром, ветви направлены вниз.
а)найти координаты вершины (для построения):
х₀= -b/2a = 2/-2= -1;
у₀=-(-1)²-2*(-1)+3= -1+2+3=4;
Координаты вершины параболы (-1; 4).
б)найти нули функции, точки пересечения параболой оси Ох (для построения графика).
Для этого нужно приравнять уравнение к нулю и решить квадратное уравнение:
-х²-2х+3=0
х²+2х-3=0
D=b²-4ac = 4+12=16 √D= 4
х₁=(-b-√D)/2a
х₁=(-2-4)/2
х₁= -6/2
х₁= -3;
х₂=(-b+√D)/2a
х₂=(-2+4)/2
х₂=2/2
х₂=1
Координаты точек пересечения параболой оси Ох (-3; 0) (1; 0).
Дополнительные точки. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -5 -4 -3 -2 -1 0 1 2 3
у -12 -5 0 3 4 3 0 -5 -12
2)Найти промежуток убывания.
Согласно графика, функция убывает при х от -1 до + бесконечности, х∈(-1, +∞).
3)Найти множество решений неравенства -х²-2х+3 <=0
Согласно графика, у<=0 при х∈(-∞, -3]∪[1, +∞).