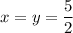Переписывая уравнение в виде y=-(x-2)²+3=-x²+4x-1, замечаем, что график представляет собой квадратическую параболу. Так как коэффициент при x² равен -1<0, то ветви параболы направлены вниз. Первый член -(x-2)² обращается в 0 лишь при x=2, а пи других значениях х он отрицателен. Поэтому точка x=2 является вершиной параболы, в которой функция достигает своего наибольшего значения Ymax=y(2)=-2²+4*2-1=3. То есть координаты вершины есть (2;3). Чтобы найти координаты точек пересечения параболы с осью ОХ, надо решить уравнение x²-4x+1=0. Находим дискриминант D=(-4)²-4*1*1=12=(2√3)². Тогда x1=(4+2√3)/2=2+√3, x2=(4-2√3)/2=2-√3. Значит, (2+√3;0) и (2-√3;0) - координаты точек пересечения параболы с осью ОХ. Отсюда ясно, что если с>3, то прямая y=c не пересекает параболу, при c=3 прямая y=3 имеет с параболой одну общую точку - вершину параболы. А при c<3 прямая пересекает параболу в 2 точках. ответ: при c<3.
ВвоыоФункция arcsin(x) обозначает угол, синус которого равен х. Это можно записать математически: sin(arcsin(x))=x. Справедливо и обратное: arcsin(sin(x))=x. Функция arcsin(x) - нечетная, как и обратная ей функция sin(x). Это значит, что arcsin(-x) = - arcsin(x). Поэтому arcsin(-3/4) = -arcsin(3/4). В принципе, arcsin(3/4) - это иррациональное число, выражающее некоторый вполне конкретный угол, заданный именно таким выражением. Но если тебя не устраивает такая запись, можно найти приближенное значение при инженерного калькулятора
x + y = 5 отсюда y = 5 - x.
Рассмотрим функцию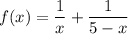
Производная функции: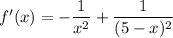
и приравняем ее к нулю.
(0)____-_____(2.5)____+___(5)___+___
В точке x = 2.5 производная функции меняется знак с (-) на (+), следовательно, x = 2.5 - относительный минимум.
y = 5 - 2.5 = 2.5
ответ: при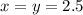
выражение 
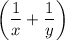принимает наименьшее значение.
Второй без производной)
Для x,y> 0 применим неравенство Коши
При этом равенство достигает наименьшего значения при