Р = 28 см.
Объяснение:
По условию смежные стороны прямоугольника относятся как 3:4.
Обозначим одну часть через x.
Тогда ширина прямоугольника будет равна 3х, т.к. осоставляет 3 таких части, а длина прямоугольника будет равна 4х, т.к. оставляет 4 таких части.
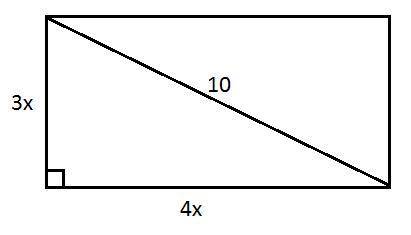
Диагональ в прямоугольнике с двумя смежными сторонами образует прямоугольный треугольник (см. рисунок). Диагональ равна 10 см.
Воспользуемся теоремой Пифагора и составим уравнение.
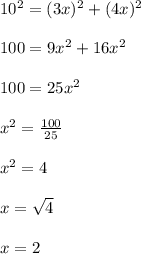
Ширина прямоугольника: 3х = 3·2 = 6 (см).
Длина прямоугольника: 4х = 4·2 = 8 (см).
 (см)
(см)
Р = 28 см.
Объяснение:
По условию смежные стороны прямоугольника относятся как 3:4.
Обозначим одну часть через x.
Тогда ширина прямоугольника будет равна 3х, т.к. осоставляет 3 таких части, а длина прямоугольника будет равна 4х, т.к. оставляет 4 таких части.
Диагональ в прямоугольнике с двумя смежными сторонами образует прямоугольный треугольник (см. рисунок). Диагональ равна 10 см.
Воспользуемся теоремой Пифагора и составим уравнение.
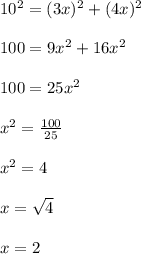
Ширина прямоугольника: 3х = 3·2 = 6 (см).
Длина прямоугольника: 4х = 4·2 = 8 (см).
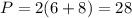 (см)
(см)

1)27^2х=81
(3^3)^2х=3^4
3^6х=3^4
6х=4
Х6/4
Х=3/2
Х=1,5
2)4^(х-3)=(1/16)^(2х+5)
4^(х-5)=(4^(-2))^(2х+5)
Х-5=-2*(2х+5)
Х-5=-4х-10
Х+4х=-10+5
5х=-5
Х=-1
3)25^(х-4)<=5
(5^2)^(х-4)<=5
2*(х-4)<=1
2х-8<=1
2х<=1+8
2х<=9
Х<=9/2
Х<=4,5
(-бесконечности;4,5]
4)9^(х-10)*3^(х+9)=(3^2)^(х-10)*3^(х+9)=3^2(х-10)+(х+9)=
=3^(2х-20+х+9)=3^(3х-11)