а) √49*2;
б)√9*11;
в)- √4*6;
г) -√100*5,
№2.
а)√36с;
б)√1/9*27а;
в)-√0,04*10х;
г)√49*1/7н
Объяснение:
так, рассмотрим этот пример:
Пример 3, упростить выражение:
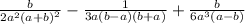
здесь, автор пытался донести, что нам нужно домножить на определенные числа, дабы получить общий знаменатель 6а³(а-b)(a+b)²
При этом, он имел ввиду, что умножение на второй знаменатель можно произвести по разному:
1) если использовать общий множитель
6а³(b-a)(a+b)² , то домножить нужно на 2а²(а+b), и это действительно не принципиально, но тогда третий множитель будет "страдать" - нужно будет домножить его уже со знаком "-": -(a+b)², чтобы при умножении, как вы и сказали: (а-b) = -(b-a) и при умножении двух минусов, мы получаем знак "+"
, так и наоборот для второго случая:
2)если использовать общий множитель
6а³(а-b)(a+b)² , то домножить второй знаменатель нужно на -2а²(а+b)!
А третий на (a+b)², с плюсовым перед стоящим знаком.
И не забываем так же про первый знаменатель :)
Тут всё дело в том, какой общий множитель вы захотите использовать.
Надеюсь, понятно объяснил.
3√11= √9*11= √99
-2√6= -√4*6= - √24
-10√5= - √100*5= - √500
6√с= √36с
1/3√27а= √1/9*27а=√3а
-0.2√10х=-√0.04*10х= -√0.4х
7√1/7n= √49/7n= √7/n или если последнее имело вид
в следующий раз точнее пишите задание.
Если хотите получить точный развернутый ответ пишите точные развернутые описания задач