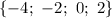x^2+2x/(x+1)^2=0
ОДЗ(Область допустимых значений):x≠-1
x^2+2x=0
x(x+2)=0
x1=0
x2=-2
ответ: x1=0; x2=-2
ответ: (0; -6)
Объяснение:
1)Найдём абсциссы точек пересечения графика с осью абсцисс:
x⁴+x²-2=0
пусть х²=у≥0 ⇒ у²+у-2=0
D=1+8=9>0
y₁= (-1+3)/2=1
y₂=(-1-3)/2=-2<0 (не удовл условию у≥0)
Если у=1, то х²=1 ⇒ х₁=1, х₂=-1 (абсциссы точек пересечения графика с осью абсцисс)
2)Найдём уравнение касательной к кривой y=x⁴+x²-2 в точке с абсциссой x₀₁ = 1.
Запишем уравнения касательной в общем виде:
y = y₀ + y'(x₀)(x - x₀)
По условию задачи x₀₁= 1, тогда y₀ = 1⁴+1²-2=0
Теперь найдем производную:
y' = (x⁴+x²-2)' = 4х³+2x
следовательно: y'(x₀)=у'(1) = 4·1³+2·1 = 6
Тогда уравнение касательной в точке с абсциссой х₀₁=1:
y=0+6·(x-1)=6х-6 или y = 6·x-6 (уравнение первой касательной)
3) Найдём уравнение касательной к кривой y=x⁴+x²-2 в точке с абсциссой x₀₂ = -1.
По условию задачи x₀₂= - 1, тогда y₀=y₀₂ = 1⁴+1²-2=0
y' = 4х³+2x
следовательно: y'(x₀₂)=у'(-1) = 4·(-1)³+2·(-1) = -6
Тогда уравнение касательной в точке с абсциссой х₀₂=-1:
y=0-6·(x+1)=-6х-6 или y = -6·x-6 (уравнение второй касательной)
4)Найдём точку пересечения этих касательных:
6х-6= -6х-6
12х=0
х=0 ⇒ у=6·0-6= -6 ⇒ (0; -6) точка пересечения этих касательных
а) 14 - (2 + 3х - х²) = х² + 4х - 9
14-2-3x+x²=x²+4x-9
14-2-3x=4x-9
12-3x=4x-9
12-3x-4x+9=0
21-7x=0
21=7x
x=21:7
x=3
6а²-(9а²-5аb)+(3a²-2ab)
а=-0,15,b=6
Думаю, что будет легче, если мы приведем подобные:
6а²-9а²+5аb+3a²-2ab (перед знаком минус - знаки в скобке меняем на противоположные, а при плюсе оставляем все, как есть)
Теперь выделяем подобные, имеющие одинаковые переменные и их степени(так будет удобней):
6а²-9а²+5аb+3a²-2ab
__ ___ __
И вычисляем:
6а²-9а²+3a²=0, поэтому мы не пишем числа, связанные с переменной а²
5аb-2аb=3аb
3аb
а и b числа:
-3 *0.15*6= -18*0.15=-2.7
ответ: -2.7
Объяснение:
ответ: