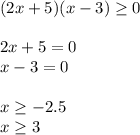
тогда область определения этой функции это интервал от x ⊂ (-∞;-2.5]∪ [3;+∞)
72км
Объяснение:
1-й мотоциклист, проехав расстояние от А до В, повернул и проехал от В 12км, пока не встретил 2-го мотоциклиста. Возьмем х за расстояние, которое проехал 2-й мотоциклист до встречи с 1-м. Следовательно расстояние от А до В, которое возьмем за у будет равным:
у=х+12.
Когда на обратном пути 1-й мотоциклист, проехав (1/6 у)км расстояния от А, встречает 2-го мотоциклиста (не обгоняет!). Значит расстояние между А и В будет равным:
у=х +1/6 у.
Составляем систему уравнений:
у=х+12
у=х +1/6 у
х+12-х -1/6 у=у-у
12 -1/6 у=0
1/6 у=12
у=12•6=72км - расстояние между пунктами А и В.
х = 32, у = 29.
Объяснение:
Записываем условие:
x - y = 3
x^2 - y^2 = 183
Выражаем y через х из первого уравнения.
y = x - 3
Заменяем y во втором уравнении.
x^2 - (x - 3)^2 = 183
Раскрываем x - 3 по правилу сокращенного умножения
(a - b)^2 = a^2 - 2ab + b^2
(x - 3)^2 = x^2 - 6x + 9
Записываем все в одно уравнение:
x^2 - (x^2 - 6x + 9) = 183
Раскрываем скобки, меняя знаки.
x^2 - x^2 + 6x - 9 = 183
6x - 9 = 183
6x = 192
x = 192/6 = 32
Следовательно y = x - 3 = 32 - 3 = 29.
Проверяем:
32 - 29 = 3
32^2 = 1024; 29^2 = 841; 1024 - 841 = 183
Все верно.
Подкоренное выражение корня чётной степени должно быть неотрицательным, то есть ≥ 0.
(2x + 5)(x - 3) ≥ 0
2(x + 2,5)(x - 3) ≥ 0
(x + 2,5)(x - 3) ≥ 0
+ - +
__________[- 2,5]___________[3]___________
x ∈ (- ∞ ; - 2,5] ∪ [3 ; + ∞)