1)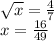
2)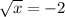
x∈∅ Утверждение ложно для любого значения х, поскольку функция корня с четным натуральным показателем всегда положительна или 0
3) x²=49
x=±7
x=7 x=-7
4) x²=-9 x∈∅ Утверждение ложно для любого значения х, поскольку функция корня с четным натуральным показателем всегда положительна или 0
5) 9√3 -5√3 +6√3=10√3
6)1) 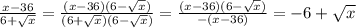
6)2) 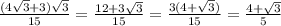
Семья в жизни каждого человека играет огромную роль. Если она есть – он счастлив, у него есть опора в жизни, есть для кого жить, за кого переживать, с кем делить удачи и неудачи. Если ее нет – человек несчастен.
У нас все доверяют друг другу переживают за всех, делятся своими мечтами и секретами. С папой, с мамой и двумя сестрами мы проводим выходные дни. Моя мама самая лучшая и красивая, ею я очень дорожу. Хоть и бывает, что мы ругаемся, но это не надолго. Папа меня любит больше всех, он самый добрый человек на Земле! Со старшей сестрой я очень редко встречаюсь, мы никогда не ругаемся, но она всегда рада мне. Второй сестре я могу рассказать абсолютно все свои секреты, я знаю, что она их никому не расскажет, она - моя лучшая подруга. Всех родных я очень люблю и берегу.
Семья подарена человечеству Аллахом. Ведь не зря он создал Адама и Еву и послал их на планету Земля. Наверное, для того, чтобы они создали семью, а все остальные потомки продолжали их род.
Человечество должно быть благодарно Аллаху за это! Ведь без семьи не было бы современного общества, в котором мы живем.
Объяснение:
дай
Пусть функция 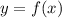 возрастает на всей области определения.
возрастает на всей области определения.
Предположим, что для некоторых значений аргумента 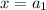 и
и 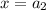 выполняется соотношение
выполняется соотношение 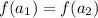 . Рассмотрим три ситуации:
. Рассмотрим три ситуации:
1. 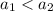 - но по определению возрастающей функции меньшему значению аргумента соответствует меньшее значение функции:
- но по определению возрастающей функции меньшему значению аргумента соответствует меньшее значение функции: 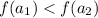 - противоречие вышеприведенному равенству значений функции
- противоречие вышеприведенному равенству значений функции
2.  - две точки равны между собой, значит и значения функции в них также равны, вышеприведенное равенство выполняется
- две точки равны между собой, значит и значения функции в них также равны, вышеприведенное равенство выполняется
3. 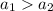 - аналогично, по определению возрастающей функции большему значению аргумента соответствует большее значение функции:
- аналогично, по определению возрастающей функции большему значению аргумента соответствует большее значение функции: 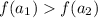 - противоречие вышеприведенному равенству значений функции
- противоречие вышеприведенному равенству значений функции
Таким образом, при любых 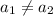 не может выполняться равенство
не может выполняться равенство 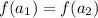 . Это означает, что возрастающая функция не может принимать одно и то же значение в двух различных точках. Или по другому, возрастающая функция принимает каждое свое значение только в одной точке.
. Это означает, что возрастающая функция не может принимать одно и то же значение в двух различных точках. Или по другому, возрастающая функция принимает каждое свое значение только в одной точке.
Для убывающей функции доказательство аналогичное с той лишь разницей, что случаю 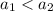 соответствует условие
соответствует условие 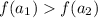 , а случаю
, а случаю 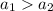 - условие
- условие 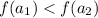 . Но опять же, разным значениям аргумента не могут соответствовать равные значения функции.
. Но опять же, разным значениям аргумента не могут соответствовать равные значения функции.
Задание 4:
1) x = 16/49;
2) Корней нет
3) x = 7 или x = -7
4) Нет корней
Задание 5:
√243 = 9√3;
3√12 = 6√3
9√3+6√3-5√3 = 10√3
Задание 6:
1) (√x-6)(√x+6)/√x+6 = √x - 6
2) √3(4+√3)/5√3 = 4+√3/5