Объяснение:
Система уравнений:
x/2 +y/2 -2xy=16 |×2
x+y=-2
x+y-4xy=32
-2-4xy=32
-4xy=32+2
-4xy=34 |2
x=-17/(2y)
-17/(2y) +y=-2
(-17+2y²)/(2y)=-2
-17+2y²=-4y
2y²+4y-17=0; D=16+136=152
y₁=(-4-2√38)4=(-2-√38)/2
y₂=(-4+2√38)4=(√38 -2)/2
x₁+(-2-√38)/2=-2; x₁=(-4+2+√38)/2=(√38 -2)/2
x₂+(√38 -2)/2=-2; x₂=(-4-√38 +2)/2=(-2-√38)/2
ответ: ((√38 -2)/2; (-2-√38)/2); ((-2-√38)/2; (√38 -2)/2).
Система уравнений:
x/2 +y/2 +2xy=4
x-y=4
x/2 +y/2 +2xy=x-y |×2
x+y+4xy=2x-2y
4xy=2x-2y-x-y
4xy=x-3y
x-4xy=3y
x(1-4y)=3y
x=(3y)/(1-4y)
(3y)/(1-4y) -y=4
(3y-y+4y²)/(1-4y)=4
2(y+2y²)=4(1-4y) |2
2y²+y-2+8y=0
2y²+9y-2=0; D=81+16=97
y₁=(-9-√97)/4
y₂=(-9+√97)/4=(√97 -9)/4
x₁ -(-9-√97)/4=4; x₁=(16-9-√97)/4=(7-√97)/4
x₂ -(√97 -9)/4=4; x₂=(16+√97 -9)/4=(7+√97)/4
ответ: ((7-√97)/4; (-9-√97)/4); ((7+√97)/4; (√97 -9)/4).

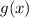 ;
; ;
; и будет искомой фигурой.
и будет искомой фигурой.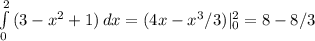
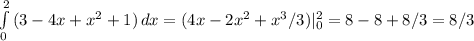
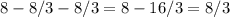 (кв. ед.)
(кв. ед.)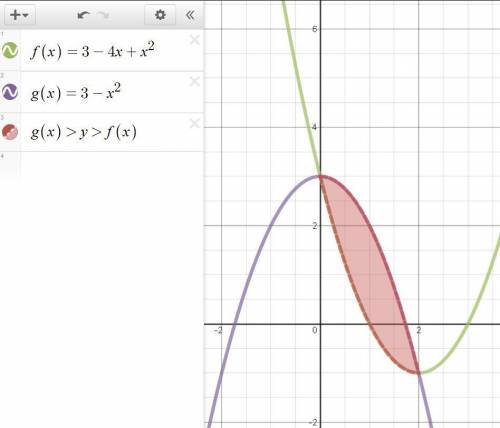
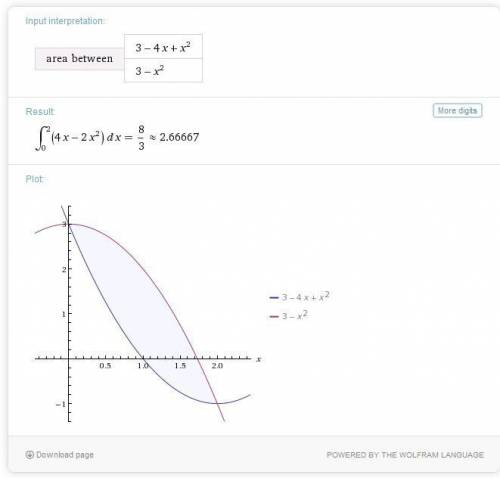
Для решения задачи в первую очередь нужно построить график.
По графику видно, что найти нужно площадь области, лежащей над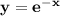 и под
и под 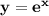 .
.
Найдём точку пересечения данных кривых. Для этого нужно решить систему из уравнений их функций.
По графику прямая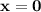 будет являться границей фигурой слева, а прямая
будет являться границей фигурой слева, а прямая 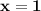 — справа.
— справа.
Найти площадь фигуры, ограниченной сверху графиком функции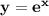 , а снизу функцией
, а снизу функцией 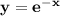 , а так же прямыми
, а так же прямыми 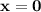 и
и 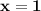 , значит вычислить следующий определённый интеграл.
, значит вычислить следующий определённый интеграл.
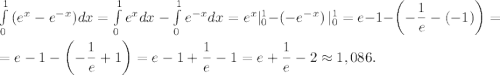
ответ: