Если sin²(x) = 0, то cos²(x) по данному уравнению тоже должен быть равен нулю. Но из основного тригонометрического тождества sin²(x) + cos²(x) = 1. Получено противоречие, ведь 0 + 0 ≠ 1. Отсюда sin²(x) ≠ 0, значит имеем право делить на него.
Направим из точки А в точку В вектор и обозначим его с, поскольку он лежит напротив точки С. Аналогично вектор, направленный из точки А в точку С обозначим b. Найдем координаты этих векторов. Получили Определим косинус угла между этими векторами: В знаменателе произведение модулей, которое всегда имеет положительное значение, следовательно значение дроби будет отрицательным. Косинус на отрезке [0;π] имеет отрицательное значение в области (π/2;π), следовательно угол А - тупой. Поэтому треугольник АВС - тупоугольный.
Для начала посмотрим на остатки от деления на 3. Правая часть делится на 3, тогда и левая часть делится на 3. 1) Если x = 3k, левая часть даёт остаток 0 - 0 - 1 = -1 ~ 2 при делении на 3, так что таких целых корней у уравнения нет. 2) Если x = 3k - 1, остаток левой части равен: -1 + 1 - 1 = -1 ~ 2, опять левая часть не делится на 3. 3) Если x = 3k + 1, остаток левой части равен: 1 - 1 - 1 = -1 ~ 2, снова не делится.
Получили, что при любом значении x левая часть на 3 не делится, а правая делится. Тогда целочисленных решений у данного уравнения нет.
Остатки можно было бы не находить перебором, а заметить, что x^3 - x = (x - 1) x (x + 1) делится на 3.
Если sin²(x) = 0, то cos²(x) по данному уравнению тоже должен быть равен нулю. Но из основного тригонометрического тождества sin²(x) + cos²(x) = 1. Получено противоречие, ведь 0 + 0 ≠ 1. Отсюда sin²(x) ≠ 0, значит имеем право делить на него.
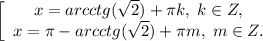
ответ: