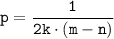
То перевернём это выражение так, что:
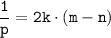
Разделим оба выражения на 2k:
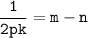
И перенесём n влево:

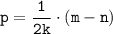
То домножим всё на 2k:
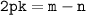
И перенесём n влево:

Выражение: 3/4=(x+2)/8
ответ: 0.5-x/8=0
Решаем по действиям:
1) 3/4=0.75
3.0|4_ _
2_8_|0.75
20
2_0_
0
2) (x+2)/8=x/8+2/8
3) 2/8=0.25
2.0|8_ _
1_6_|0.25
40
4_0_
0
4) 0.75-(x/8+0.25)=0.75-x/8-0.25
5) 0.75-0.25=0.5
-0.75
_0_._2_5_
0.50
Решаем по шагам:
1) 0.75-(x+2)/8=0
1.1) 3/4=0.75
3.0|4_ _
2_8_|0.75
20
2_0_
0
2) 0.75-(x/8+2/8)=0
2.1) (x+2)/8=x/8+2/8
3) 0.75-(x/8+0.25)=0
3.1) 2/8=0.25
2.0|8_ _
1_6_|0.25
40
4_0_
0
4) 0.75-x/8-0.25=0
4.1) 0.75-(x/8+0.25)=0.75-x/8-0.25
5) 0.5-x/8=0
5.1) 0.75-0.25=0.5
-0.75
_0_._2_5_
0.50
Решаем уравнение 0.5-x/8=0:
Решаем относительно x:
x=(-(-0.5))*8=0.5*8=4.
3.
√x +√y=5 ;
x-y =10
Область определения x≥ 0 ; y≥ 0
x-y = (√x -√y)( √x +√y)=10 ,
тогда система
√x +√y=5 ;
(√x -√y)( √x +√y)=10
подставим √x +√y=5
√x +√y=5 ;
√x -√y =2
Решим сложения
2√x = 7 ; √x = 7/2 ; x = 49/4= 12,25
x-y =10 ; y=x-10= 12,25-10= 2,25
ответ (12,25 ; 2,25)
4.
√x -√y=4 ;
x-y =24
Область определения x≥ 0 ; y≥ 0
x-y = (√x -√y)( √x +√y)=24 ,
тогда система
√x -√y=4 ;
(√x -√y)( √x +√y)=24
подставим √x -√y=4
√x -√y=4 ;
√x +√y =6
Решим сложения
2√x = 10 ; √x = 5 ; x =25
x-y =24 ; y=x-24= 25-24= 1
ответ (25 ; 1)
5.
x+y=2 ;
√(x+2) +√(3-y)=3
Область определения
x+2 ≥ 0 ; x ≥ -2
3-y≥ 0 ; 3 ≥ y
x-y = (√x -√y)( √x +√y)=24 ,
преобразуем
x+y=2 ; (x+2)-(3-y) = 1 ; (√(x+2) -√(3-y))* (√(x+2) +√(3-y)) =1
но √(x+2) +√(3-y)=3
тогда система
√(x+2) -√(3-y)=1/3
√(x+2) +√(3-y)=3
Решим сложения
2√(x+2) =1/3+3=10/3 ; √(x+2) =5/3 ; x+2 =25/9 ; x=7/9
x+y=2 ; y=2-x =2-7/9=11/9
ответ (7/9 ; 11/9)
m-n=p:1/2k
m-n=2p/k
m=2p/k+n