1) по теореме косинусов имеем: a² = b² + c² - 2bc cos a = 25 - 24 cos 135° = 25 + 12√2 a = √(25 + 12√2) по теореме синусов, a / sin a = b / sin b sin b = sin a · b / a = √2 / 2 · 3 / √(25 + 12√2) = 3 / √(50 + 24√2) ∠b = arcsin(3 / √(50 + 24√2)) ∠c = 180° - 135° - ∠b = 45° - arcsin(3 / √(50 + 24√2)) 2) ∠a = 180° - ∠b - ∠c = 65° по теореме синусов b / sin b = a / sin a b = a sin b / sin a = 24.6 · √2 / 2 / (sin 65°) = 123√2 / (10 sin 65°) по теореме синусов c / sin c = a / sin a c = a sin c / sin a = 24.6 ·sin 70° / sin 65°
Пусть скорость первого-х км/ч, а скорость второго- y км/ч Так как первый велосипедист проезжает за 3 ч на 18 км больше,чем второй за 2 ч. , то 3x- 2y=18 Так как расстояние между городами равно 52 км и велосипедисты встретились через 2 ч после начала движения, то 2(x+y)=52 Получили систему уравнений:3x-2y=18 и 2(x+y)=52 2(x+y)=52 x+y=26 x=26-y Подставляем значение х в уравнение 3x-2y=18 3(26-y)-2y=18 78-3y-2y=18 -5y=-60 y=12(км/ч)-скорость второго x=26-y x=26-12 x=14(км/ч)-скорость первого велосипедиста.
Если
, то 
. То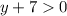гда
P.S. Если
, то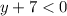 
. Тогда