Парабола – график квадратичной функции. Этот график позволяет прослеживать основные свойства функции в зависимости от вида квадратичной функции.
Существуют различные преобразования графиков, если тебе нужно узнать поподробнее об этом напиши в комментариях и я объясню.
Мы рассмотрим только все самое основное.
В функции y= a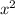
От коэффициента а зависит то куда направлены ветви параболы и то, как они идут.
Если коэффициент а>0, тогда ветви будут идти вверх.
Если коэффициент а<0, тогда ветви будут идти вниз.
От этого коэффициента и зависит то, как они выглядят.
Если коэффициент больше 1, то парабола будет идти резче вверх, а то, насколько он больше 1 будет показателем того насколько она идет резче по оси оу.
Если коэффициент больше 0, но меньше 1, то парабола будет более прижатой к оси абсцисс (ох), а коэффициент будет показателем того насколько она прижата к оси.
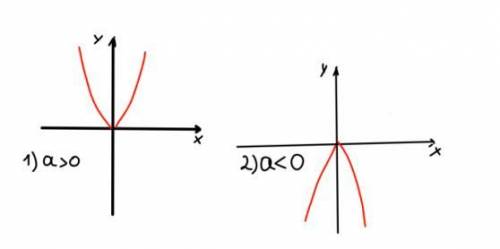
Для этого на примере рассмотрим графики функций у=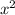 , у=2
, у=2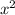 и у=
и у=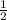
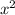
Заранее прощения не за самые ровные графики.
На этом графике мы видим подтверждение ранее сказанного правила.
По функции можно сразу определять каким будет график параболы.
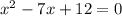
разложим с группировки
Рассмотрим x²+bx+c
. Найдем пару целых чисел, произведение которых равно c, а сумма равна b. В данном случае произведение равно 12, а сумма равна -7
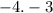
Запишем разложение на множители, используя эти целые числа.
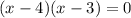
Если любой отдельный множитель в левой части уравнения равен 0 ,то и все выражение будет равняться 0.
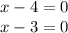
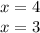
Используем каждый корень для создания проверочных интервалов.
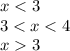
Выбираем тестовое значение из каждого интервала и подставляем его в начальное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.
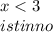
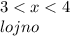
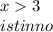
Решение включает все истинные интервалы.
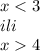
Результат можно выразить в различном виде.
Форма неравенства:
x < 3 или x > 4
Запись в виде интервала:
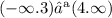
(х+2)(х-2)(х^2+4)-(4+х^2)^2=(х^2-4)(х^2+4)-(16+8х^2+х^4)=х^4-16-16-8х^2-х^4=-8х^2-32= -8(х^2+4)
Если х=1/2=0,5, то -8(х^2+4)=-8(0,5^2+4) =-8(0,25+4) =-8*4,25=-34