3x^2 + 6x - 5x - 10 - x^2 + 5x + 2≤ 0
2x^2 + 6x - 8 ≤ 0
x^2 + 3x - 4≤ 0
1) ветки вверх
2) нули функции:
x^2 + 3x - 4 = 0
D = 9 - 4×(-4) = 9 + 16 = 25
x1 = (- 3 + 5)/2 = 1
x2 = (- 3 - 5)/2 = - 4
x∈ включительно от -4 до 1
ответ: целые решения неравенства: -4, - 3, -2, -1, 0, 1( шесть целых решений)
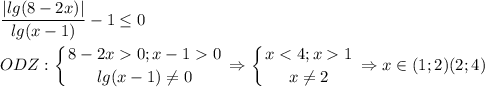
1) раскроем модуль при lg(8-2x)≥0
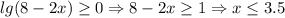
тогда
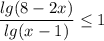
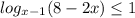
далее применим метод рационализации
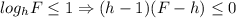
получаем
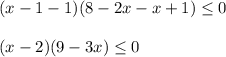
и метод интервалов
x=2; x=3
___-_____2__+____3___-___
1 по условию 3,5
тогда в первом случае x∈ (1;2)∪ [3;3.5]
2) раскроем модуль lg(8-2x)<0
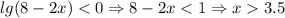
тогда
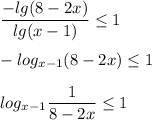
метод рационализации
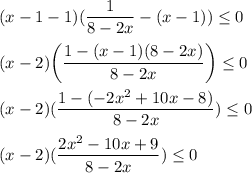
x=2; x≠4; x= 2.5 ±0,5√7 (это х ≈ 3,82 и х≈1,17)
_-___2,5-√7___+___2_____-______2,5+0,5√7__+____4___-___
3,5 по условию 4
тогда во втором случае х∈(3,5; 2.5+0.5√7]
3) и теперь все объединяем
х∈ (1;2)∪ [3; 2.5+0.5√7]
(3x - 5)(x + 2) ≤ x² - 5x - 2
3x² + 6x - 5x - 10 ≤ x² - 5x - 2
3x² + x - 10 - x² + 5x + 2 ≤ 0
2x² + 6x - 8 ≤ 0
x² + 3x - 4 ≤ 0
(x + 4)(x - 1) ≤ 0
+ - +
[- 4][1]
x ∈ [- 4 ; 1]
Целые решения : - 4 ; - 3; - 2; -1; 0; 1