Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле: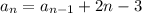
, где n - число лучей кратное 3.
Пробуем вычислить по этой формуле:
Итак, ответ найден. Для 27 лучей возможно максимум 243 тупых угла.
Так считать долго, можно увидеть формулу для прямого расчёта: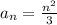
По этой формуле можно считать для любого количества лучей, кратное трём.
Нужно воспользоваться формулой разности квадратов практически во всех примерах: (a - b)(a + b) = a² - b².
Выполните умножение:
1) 5b(b - 1)(b + 1) = 5b(b² - 1) = 5b³ - 5b;
2) (c + 2)(c - 2) · 8c² = (c² - 4) · 8c² = 8c⁴ - 32c²;
3) (m - 10)(m² + 100)(m + 10) = (m - 10)(m + 10)(m² + 100) =
= (m² - 100)(m² + 100) = m⁴ - 10 000;
4) (a² + 1)(a² - 1)(a⁴ + 1) = (a⁴ - 1)(a⁴ + 1) = a⁸ - 1;
Упростите выражение:
1) (x + 1)(x - 1) - (x + 5)(x - 5) + (x + 1)(x - 5) = x² - 1 - (x² - 25) + x² - 5x + x - 5 = x² - 1 - x² + 25 + x² - 4x - 5 = x² - 4x + 19;
2) 81a⁸ - (3a² - b³)(9a⁴ + b⁶)(3a² + b³) = 81a⁸ - (3a² - b³)(3a² + b³)(9a⁴ + b⁶) = 81a⁸ - (9a⁴ - b⁶)(9a⁴ + b⁶) = 81a⁸ - (81a⁸ - b¹²) = 81a⁸ - 81a⁸ + b¹² = b¹².
Здравствуйте!
Путь F(x) = log2 (x-5), а G(x) = log3 (x)
Найдём D(f) : x-5>0 x>5 D(g): x>0
Так как F(x) монотонно возрастает на всей области допустимых значениях (D(f)) и G(x) монотонно возрастает на всей области допустимых значениях (D(g)), то и сумма F(x) + G(x) монотонно возрастает на области допустимых значениях этих функций, то есть на области полученное путём пересечения допустимых значениях D(f) и (D(g)) - x>5 и x>0 => x>5
Таким образом функция T(x) = F(x) + G(x) монотонно возрастает на всей области допустимых значениях (x>5) и так как это логарифмическая функция (график можете найти в интернете), то она пересечёт прямую a = 4 лишь в 1 точке => уравнение log2 (x-5) + log3 (x) = 4 имеет 1 корень. Данный корень легко найти подбором x = 9. => решение неравенства (так как нам надо меньше этого корня) является интервал (5;9)
ответ: (5;9)