Question

Решить возвести в степень и вычислить

Answer 1

Объяснение:

Итак, вспоминаем алгебру 7-го класса.

Для того, чтобы перемножить алгебраические дроби, необходимо разложить на множители числитель и знаменатель. Благо, раскладывать на множители нам надо только в числителе второй дроби. Мы видим, что a² - n² - это формула разности квадратов(формулы сокращенного умножения надо выучить, иначе ты не сможешь осилить дальнейший курс алгебры!). Раскладываем формулу: (a - n)(a + n).

Получаем дроби:

$\frac{3an}{2(a + n)} * \frac{(a - n) (a + n)}{3}$

3 в числителе первой дроби и 3 в знаменателе второй дроби сократятся, (a + n) в числителе второй дроби и (a + n) в знаменателе первой дроби сократятся.

Останется:

$\frac{a - b}{2}$

№2.

(a + x) * $\frac{ax}{(a + x)(a^2 - ax + x^2}$

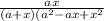
Обрати внимание: мы в знаменателе второй дроби раскрыли формулу, которая называется сумма кубов(выучи формулы сокращенного умножения!).

(a + x) сократится, останется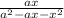 $\frac{ax}{a^2 - ax - x^2}$

№3.

Опять же, вспомним алгебру 7 класса, а именно свойства степеней.

Нам нужно одно свойство степеней, а именно:

$(\frac{a}{b} )^n = \frac{a^n}{b^n}$

Формулируем свойство: если нам требуется возвести дробь в энную степень, то в эту энную степень возводится и числитель и знаменатель.

Воспользуемся этим:

xc возводим в пятую степень:

x^5c^5

(^5 - это степень)

Возводим знаменатель в степень:

a^5y^5(c+x)^5

ответ: x^5c^5/a^5y^5(c+x)^5