Допустим, что  . Тогда имеем уравнение
. Тогда имеем уравнение  , не имеющее решений, поскольку в левой части число неположительное, а в правой - положительное, т.е. левая часть никак не может быть равна правой. Т.е.
, не имеющее решений, поскольку в левой части число неположительное, а в правой - положительное, т.е. левая часть никак не может быть равна правой. Т.е. 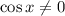
Преобразуем правую часть:
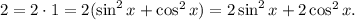
Перенесем все влево с противоположным знаком:

Поскольку 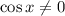 , можем разделить обе части уравнения на
, можем разделить обе части уравнения на  . В итоге имеет равносильное исходному уравнение
. В итоге имеет равносильное исходному уравнение

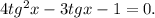
Заметим, что 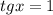 является корнем уравнения относительно тангенса. Тогда по теореме Виета второй корень равен
является корнем уравнения относительно тангенса. Тогда по теореме Виета второй корень равен 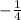 .
.
Соответственно, имеем два случая: или  или
или 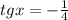 .
.
1 случай.
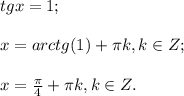
2 случай.
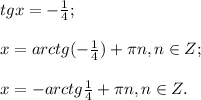
Имеем две серии корней.
ОТВЕТ: π/4 + πk, k ∈ Z; -arctg(1/4) + πn, n ∈ Z.
Найдите площадь круга, вписанного в треугольник со сторонами 18 см, 24 см , 30 см.
" решение " S =πr² , где радиус вписанной окружности
a = 6*3 ; b=6*4 ; c =6*5 ⇒треугольник (пусть ABC) прямоугольный
и не только ( Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.)
г = (a+b-c) /2 = (18 +24 -30)/2 см = 12/2 см = 6 см
S = πr² = 36π см² || 113 ,0971... см² , 113 ,1 см² ||
ответ: 36π см²
- - - - - - - - - - - - - - - - - - - - - - - - - - -
ОБЩИЙ СЛУЧАЙ ( думаю не вредит: r = S/p )
S = P*r , где p _ полупериметр (сумма длин всех сторон поделенная на два). ⇒ r = S/p ; S =√p(p-a)(p-b)(p-c) ← (Площадь треугольника по формуле Герона) . В этой задаче p=(18+24+30)/2 =36 (см)
S =√p(p-a)(p-b)(p-c) =√(36*18*12*6)=√(36²*6²) =36*6 =216 ; r = 216/36=6
Но здесь гораздо проще S =a*b/2 =18*24/2 = 216 (Δ -прямо∠ный)
r =216 /36 =6
( ΔA₁B₁C₁ со сторонами a₁=3 ; b₁ =4; c₁=5⇒r₁=(a₁ + b₁- c₁)/2=(3+4-5)/2 = 1
r = k*r₁ , где k =a/a₁ =6 коэффициент подобия ⇒ r =6*1 = 6
* * * S =k²* S₁ ; S₁ =a₁*b₁/2 =3*4/2 = 6 ⇒ S =6²*6 =216 * * *
Первая система не имеет решений т.к.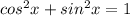 по основ. тригон. тожд., а у нас получается, что равно 0 и так же квадрат не может быть меньше 0. Тогда решаем вторую систему.
по основ. тригон. тожд., а у нас получается, что равно 0 и так же квадрат не может быть меньше 0. Тогда решаем вторую систему.
ответ: x∈[-arctg(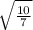 )+pi*n;arctg(
)+pi*n;arctg(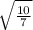 )+pi*n], n∈Z
)+pi*n], n∈Z