В решении.
Объяснение:
х² - 10х + 24
1) Выделить полный квадрат:
х² - 10х + 24 = 0
Для выделения квадрата разности не хватает квадрата второго числа, удвоенное произведение первого числа на второе показывает, что второе число должно быть равно 5, а квадрат его = 25:
(х² - 10х + 25) - 25 + 24 = 0
25 добавили, 25 надо и отнять.
Свернуть квадрат разности:
(х - 5)² - 1 = 0
2) Разложить трёхчлен на множители.
Найти х₁ и х₂:
(х - 5)² - 1 = 0
(х - 5)² = 1
Извлечь корень из обеих частей уравнения:
х - 5 = ±√1
х - 5 = ±1
х₁ = 1 + 5
х₁ = 6;
х₂ = -1 + 5
х₂ = 4;
х² - 10х + 24 = (х - 6)*(х - 4).
а) x€ (-∞;-4)U(2;+∞)
б) x€∅
Объяснение:
N°1:
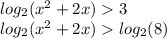
Т. к. основание логарифма 2 > основание 1 => знак неравенства не меняется
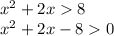
D = b²-4ac = 4+32 = 36 = 6²
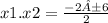
х1= 2; х2 = -4
(х-2)(х+4) > 0
х€ (-∞; -4)U(2;+∞)
ОДЗ: х²+2х > 0
х(х+2) > 0
Значит:
х€ (-∞; -2)U(0;+∞)
Получаем систему:
{x€ (-∞;-4)U(2;+∞)
{x € (-∞;-2)U(0;+∞)
Отсюда:
x€ (-∞;-4)U(2;+∞)
ответ: x€ (-∞;-4)U(2;+∞)
N°2:
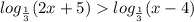
Т. к основание логарифма 1/3 < основания 1 => знак неравенства меняется
2х+5 < х-4
х <-9
Значит:
х€ (-∞; -9)
ОДЗ:
{2х+5 > 0
{х-4 > 0
Получаем:
{х> -2,5
{х>4
Значит:
х€ (4;+∞)
Получаем систему:
{х€ (-∞;-9)
{х€ (4;+∞)
Отсюда: х€∅
ответ: х€∅
x₀= -b/2a - абсцисса вершины параболы y=ax²+bx+c
y=5x^2-20x+3
a=5; b=-20
x₀= -b/2a =20/(2·5)=2
y₀=5·2²-20·2+3
y₀=-17
О т в е т. (2;-17)