1)2b³-6-4b²+3b=
2b^2(b-2)+3(b-2)=
(b-2)(2b^2+3)
2)x³-6+2x-3x²=(x^2-3)(x-3) +2(x-3)=(x-3)(x^2-3+2)=
(x-3)(x^2-1)
Так как в задаче указаны пары перчаток и все они различны, то общее количество перчаток равно 72 (в данном случае количество пар умножается на 2).
Половина из данного количества перчаток приходится на левую руку, а половина, соответственно, на правую, то есть количество перчаток, приходящихся на одну руку равно 36 (36 на левую и 36 на правую).
В связи с этим можно сделать вывод, что количество выборки из 36 перчаток, приходящихся на одну руку, равно количеству сочетаний из 36 элементов по 28.
= 
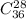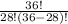= 30260340.
Так как у нас 36 перчаток приходится на одну и ещё 36 на другую, то, соответственно, нужно найденное количество сочетаний умножить на 2, тогда мы получим 60520680 сочетаний.
ответ:60520680
Стандартный вид числа представляется в виде:
число от 1 до 10 * 10 в какой-то степени. Такм образом,
0.00019 = 1.9 * 10^-4
2)Здесь сначала перенесу слагаемое из левой части уравнения в правую, а затем извлеку квадратный корень.
2x² - 8 = 0
2x² = 8
x² = 4
x1 = 2; x2 = -2
3)Для начала разложу многочлен, стоящий в левой части неравенства на множители. Для этого решу квадратное уравнение:
x² + 2x - 8 = 0
x1 = -4; x2 = 2
Значит, данное разложение имеет вид:
(x + 4)(x - 2) ≤ 0 (если я всё правильно понял со знаком неравенства).
Решу это неравенство методом интервалов. Отмечу на числовой прямой нули данного выражения, они разбивают всю область определения выражения на 3 интервала. Определю знаки на каждом интервале: + - +(по правилу чередования знаков). И найду нужные интервалы:
[-4;2]
1)
2b³-6-4b²+3b = 2b²(b - 2) + 3(b - 2) = (b - 2)(2b² + 3)
2)
x³-6+2x-3x² = х²(х - 3) + 2(х - 3) = (х-3)(х² + 2)