![2log_2^2(sinx)+3log_2(sinx)-2\geq 0\; \; ,\; \; \; ODZ:\; sinx0\\\\t=log+2(sinx)\; \; ,\; \; 2t^2+3-2\geq 0\; ,\; \; t_1=-2\; ,\; t_2=\frac{1}{2}\\\\2(t+2)(t-\frac{1}{2})\geq 0\; \; ,\; \; \; +++[-2\, ]---[\frac{1}{2}\, ]+++\\\\t\in (-\infty ,-2\, ]\cup [\, \frac{1}{2},+\infty )\\\\\left [ {{log_2(sinx)\leq -2} \atop {log_2(sinx)\geq \frac{1}{2}}} \right. \; \left [ {{sinx\leq 2^{-2}} \atop {sinx\geq \sqrt2}} \right. \; \left [ {{sinx\leq \frac{1}{4}} \atop {x\in \varnothing }} \right. \; \; \to\; \; \; 0](/tpl/images/0990/3474/c0d80.png)
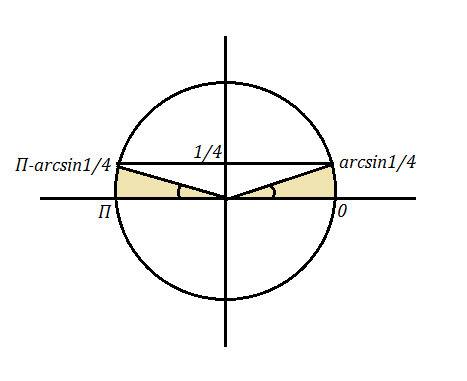
![x\in (2\pi n\, ;\, arcsin\frac{1}{4}+2\pi n\, ]\cup [\, \pi -arcsin\frac{1}{4}+2\pi n\, ;\, \pi +2\pi n\, )](/tpl/images/0990/3474/a22b9.png)
 " />
" />
Для нахождения решения корней x2 - 6x = 16 полного квадратного уравнения мы начнем с того, что перенесем 16 в левую часть уравнения:
x2 - 6x - 16 = 0.
Для решения уравнения будем использовать формулы для поиска дискриминанта и корней уравнения через дискриминант.
D = b2 - 4ac = (-6)2 - 4 * 1 * (-16) = 36 + 64 = 100;
Корни уравнения мы вычислим по следующим формулам:
x1 = (-b + √D)/2a = (6 + √100)/2 * 1 = (6 + 10)/2 = 16/2 = 8;
x2 = (-b - √D)/2a = (6 - √100)/2 * 1 = (6 - 10)/2 = -4/2 = -2.
ответ: x = 8; x = -2.
Объяснение: