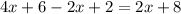
4x+6-2x+2=0
2x+8=0
2x=-8
x=-8/2
x=-4
ответ:1)Алгебраической называют дробью.
2)Тождество — это уравнение, которое удовлетворяется тождественно
3)число n (показывающее сколько раз повторяется множитель) – показателем степени
4)Квадратное уравнение называют приведенным, если его старший коэффициент равен 1.
5)Решить уравнение - значит найти все его корни или установить, что их нет.
6)Деление числителя и знаменателя на их общий делитель, отличный от
единицы, называют сокращением дроби.
7)при умножении ( делении ) числителя и знаменателя на одно и то же выражение ( число) получившаяся дробь = исходной
8)числители перемножаются отдельно
отдельно знаменатели
полученную дробь если это возможно сокращают
пример
2/3* 3/4 = (2*3)/(3*4)=6/12=1/2 (произвели сокращение на 6
9)Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.
10) Сложение и вычитание алгебраических дробей c одинаковыми
знаменателями выполняется по тому же правилу, что и с обыкновенными
дробями:
аd + bd – cd = a+b−cd .
11) Нам известно, что дробь 34 равна частному 3 : 4 ,
значит, выражение ( 14+ 15) : ( 13− 16) = ( 14+ 15)( 13− 16) .
Частное двух чисел или выражений, в котором знак деления
обозначен чертой, называют дробным выражением.
Найдем значения выражений:
а) ( 14+ 15)( 13− 16) = ( 520+ 420)( 26− 16) = ( 920)( 16) = 920 : 16 =
= 920• 61 = 5420 = 2 710 = 2,7
12)Пусть a0 и a1 - натуральные числа. Для нахождения их наибольшего общего делителя используется алгоритм Евклида [1] последовательного деления с остатком: a0=a0a1+a2, a1=a1a2+a3, a2=a2a3+a4, … ,где натуральные числа a0,a1,a2, … суть неполные частные. Это алгоритм разложения числа a =a0/a1 в правильную цепную дробь, и он применим к любым вещественным числам a. При этомa0=[a], где [a] - целая часть числа a, a1=[1/(a-a0)], … , т.е.
a=a0+ 1a1+ 1a2+ 1a3+ ···,
13)http://school.xvatit.com/images/9/92/11-06-34.jpg
14)Складываются показатели степеней при УМНОЖЕНИИ степеней с одинаковыми основаниями.
2^3+2^5=8+32=40.
Подробнее - на -
Объяснение:
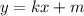: если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором 
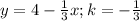. С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения 
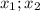, два произвольных числа, но 
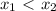. Пусть мы имеем функцию 
, тогда вычисляем значения функции в этих двух точках, имеем 
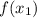и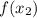 
, так вот, если 
, тогда функция возрастающая, если же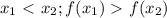 
, то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)
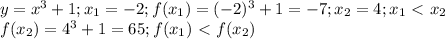, т.е. функция возрастающая. А вот задание с 
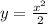не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной) 
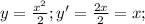. Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка): 
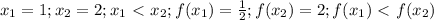, функция возрастает, что и требовалось доказать.
