ответ:45=45
Объяснение:
3x+4)(4x-3)-5=(2x+5)(6x-7)
перенесём всё в левую часть и приравняем уравнение к нулю, при этом не забываем сменить знак на противоположный
(3x+4)(4x-3)-5-(2x+5)(6x-7)=0
поочерёдно раскрываем скобки
12х²-9х+16х-12-5-(12х²-14х+30х-35)=0
12х²-9х+16х-12-5-12х²+14х-30х+35=0
группируем
(12х²-12х²)+(-9х+16х+14х-30х)+(-12-5+35)=0
-9х+18=0
9х=18
х=18:9
х=2
(3·2+4)(4·2-3)-5=(2·2+5)(6·2-7) (это проверка)
(6+4)(8-3)-5=(4+5)(12-7)
10·5-5=9·5
50-5=45
45=45
Дано уравнение cosx=1/(1- tgx).
сosx*(1 - tgx) = 1.
сosx - сosx*tgx = 1.
Заменим tgx = sinx/cosx,
сosx - сosx*( sinx/cosx) = 1.
cosx – sinx = 1.
Заменим sinx = √(1 – cos²x)
cosx - √(1 – cos²x) = 1.
Перенесём корень вправо, а 1 влево и возведём обе части в квадрат.
cos²x – 2cosx + 1 = 1 – cos²x,
2 cos²x – 2cosx = 0,
2cosx(cosx - 1) = 0.
Имеем 2 решения: cosx = 0 и cosx = 1.
Находим значения х:
x = arc cos 0 отбрасываем, так как при этом функция тангенса не имеет определения.
x = arc cos(1) = 2πn, n ∈ Z.
ответ: в заданном промежутке имеется 3 корня уравнения
-2π, 0, 2π.
.

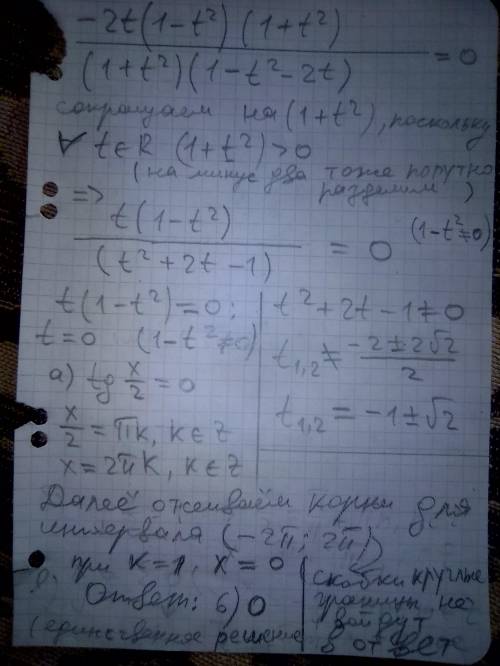

f(x)=2x-4
x=-1 y=-6
x=2 y=0
g(x)=-x+2
x=-1 y=2
x=2 y=0
f(x)>g(x)
x∈(2;∞)
f(x)<g(x)
x∈(-∞;2)