Объяснение:
Удаляем знак модуля и превращаем в квадратное уравнение: y =2*x²- 9*x- 5 ≥ 0 - квадратное уравнение.
D = b² - 4*a*c = (-9)² - 4*(2)*(-5) = 121 - дискриминант. √D = 11.
x₁ = (-b+√D)/(2*a) = (9+11)/(2*2) = 20/4 = 5 - первый корень
x₂ = (-b-√D)/(2*a) = (9-11)/(2*2) = -2/4 = -0,5 - второй корень
Это две точки где границы уравнения задачи. Записываем неравенство:
y ≥ 20 при х ∈(-∞;- 0.5]∪[5;+∞)
Наименьшее положительное - х = 5 - ответ.
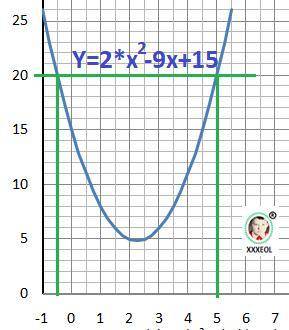
Рисунок с графиком функции показывает, что отрицательным это выражение не бывает.
ответ: за 20 минут Крис очистит класс один.
Объяснение:
из условия следует, что Роберт за 1 минуту чистит (1/30) часть класса - это его производительность (скорость работы)
обозначим за (х) минут время Криса для очистки всего класса в одиночестве; тогда производительность Криса (1/х) часть класса в минуту
вместе они очистят за 1 минуту (1/x)+(1/30) часть класса и по условию это =1/12
получили уравнение
1/x = (1/12) - (1/30)
1/x = (5-2)/60
1/x = 1/20
x = 20 минут время Криса
Проверка:
за 1 минуту Крис чистит 1/20 часть класса; вместе за 1 минуту они чистят (1/30)+(1/20) = (2+3)/60 = 5/60 = 1/12 часть класса, т.е. весь класс (это 1 целое) очистят за 12 минут