(-бесконечности ; -10] и (7; +бесконечности)
Объяснение:
Запишем все под одной дробью:
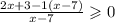
Найдём область допустимых значений:
х-7≠0, то есть х ≠ 7
Раскроем скобки и решим:
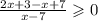
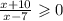
Рассмотрим все возможные случаи (знаменатель строго больше нуля, так как если он будет равен нулю, выражение потеряет смысл):
1. Когда и знаменатель, и числитель больше 0
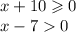
2. Когда оба меньше 0
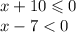
1.
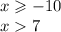
То есть х принадлежит ( 7; +бесконечности)
Так как 7 не удовлетворяет ОДЗ, то скобки круглые
2.
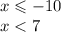
То есть х принадлежит (- бесконечности ; - 10]
Найдём объединение:
Х принадлежит (-бесконечности ; -10] и (7; +бесконечности)
Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
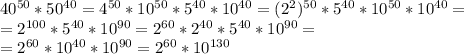
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
90 чисел.
Объяснение:
Нам подходят все натуральные числа ≤ 100.
Рассмотрим сумму двух чисел.
Заметим, что 0 нацело делится на 100.
Любая сумма чисел этого числа будет ≤18, но при этом сумма чисел этого числа всегда будет больше нуля. Поскольку 0 не является натуральным числом в математике.
Теперь рассмотрим произведение двух чисел этого числа.
где:
a принимает значения — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
b принимает значения — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Заметим, что a ≠ 0, поскольку число не может начинаться с нуля.
Рассмотрим, если b = 0, то таких чисел:
То есть, вот эти числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
Всего, подходящих нам чисел: 100 - 10 = 90 чисел.