12см и 16 см
Объяснение:
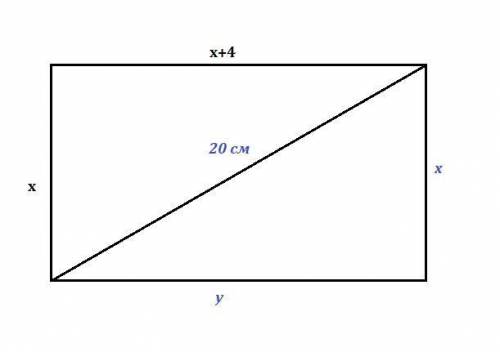
1) Пусть одна сторона прямоугольника равна х см, тогда вторая - (х+4) см. Так как в прямоугольнике все углы прямые, найдём диагональ прямоугольника по теореме Пифагора:
х²+(х+4)²=20²
2х²+8х-384=0
х²+4х-192=0
D = 4²-4*(-192)=16+768=784=28²
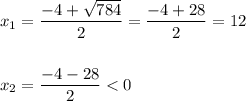
т.к. сторона не может быть меньше нуля, то меньшая сторона прямоугольника равняется 12см, большая: 12+4=16см
2) Если меньшую сторону обозначить через х см, а большую через у см, то получим следующие уравнения:
у-х=4 (одна сторона на 4 см больше от другой)х²+у²=20² (находим диагональ по т.Пифагора)Система уравнений, которая соответствует условию задачи:
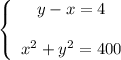

1) 3х2-х-4=0
D=(-1)^2-4*3*(-4)=1+48=49
x1=(1+7):6=1целая 2\6=1 целая1\3
х2=(1-7):6=-1
ответ:-1; 1 целая 1\3
2) 3х2-10х+3=0
D=(-10)^2-4*3*3=100-36=64
x1=(10+8):6=3
х2=(10-8):6=2\6=1\3
ответ:1\3;3.
Дальше, чтоб узнать сколько корней найдем дискриминант:
1)1) 2х ^2-х+1=0
D=(-1)^2-4*2*1=1-8=-7<0
D<0 корней нет.
2)5х2+3х-1=0
D=3^2-4*5*(-1)=9+20=29
D>0 2 корня
3)х2-10х+25=0
D=(-10)^2-4*1*25=100-100=0
D=0 1 КОРЕНЬ
2) Раскрываем скобки
3) Переносим игрик влево, а икс и цифры вправо
4) Составляем таблицу
x y
5 0
10 5
5) Рисуем систему координат
6) Отмечаем две точки (в таблице есть)
7) Соединяем их
8) Продлеваем прямую