Сначала построим график f(x)=2x+3.4
А теперь подумаем, что будет при взятии целой части числа.
Вот, допустим, f(x)=1 без взятия целой части, при 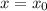 , тогда при любом
, тогда при любом 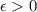
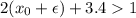 , но при взятии целой части будет 1. Далее, при некотором
, но при взятии целой части будет 1. Далее, при некотором  , f(x)=2.
, f(x)=2.
Но при любом 
При 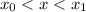 идет прямая, в
идет прямая, в 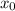 точка не выколота, а вот в
точка не выколота, а вот в  где f(x)=1 выколота, а вот где f(x)=2 не выколота.
где f(x)=1 выколота, а вот где f(x)=2 не выколота.
И так далее.
При f(x)<0 все симметрично наоборот
На рисунке я постарался отметить все, что нужно. Синяя прямая - исходная прямая графика y=2x+3.4, а вот черные кусочки - нужный график вместо с выколотыми точками.
Пунктирами, по факту, отмечены разрывы функции. Это перпендикуляры к кусочкам графика
![Постройте график функции целой части числа f(x) = [2x + 3.4].](/tpl/images/0741/6343/5cb8e.jpg)
приведем оба уравнения системы к виду y=kx+b(уравнение прямой).
Если две прямые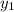 и
и  заданы уравнениями
заданы уравнениями  и
и  , то на плоскости они могут быть:
, то на плоскости они могут быть:
1) и
и  - прямые параллельны, следовательно они не пересекаются и, следовательно, система из таких прямых не имеет решений.
- прямые параллельны, следовательно они не пересекаются и, следовательно, система из таких прямых не имеет решений.
2) и
и  - прямые совпадают, следовательно, система из таких прямых будет иметь бесконечное множество решений.
- прямые совпадают, следовательно, система из таких прямых будет иметь бесконечное множество решений.
3) - прямые пересекаются в одной точке, следовательно, система из таких прямых будет иметь только одно решение.
- прямые пересекаются в одной точке, следовательно, система из таких прямых будет иметь только одно решение.
Применим это для решения данной задачи:
Значит, при a=0 данная система не имеет решений.
Значит, при a=3 данная система имеет бесконечное множество решений.
При остальных значениях a система будет иметь только одно решение:
В итоге:
ответ: a=0 => система не имеет решений(x∈∅)
a=3 => система имеет бесконечное множество решений(x∈R)
a∈(-∞;0)∪(0;3)∪(3;+∞) => система имеет одно решение.