Одночленом называют алгебраическое выражение, которое представляет собой произведение чисел и переменных, возведённых в степень с натуральными показателями.
а) a + b² не является одночленом, так как в этих алгебраических выражениях нет произведения чисел и переменных, возведённых в степень с натуральными показателями.
б)  - одночлен
- одночлен
в) 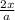 - не одночлен, объяснение такое же как в примере а)
- не одночлен, объяснение такое же как в примере а)
г) -8 является одночленом, ведь одночленами являются также все числа, любые переменные и степени переменных.
д) а - одночлен
е) 0 одночлен
ответ: а) Нет; б) Да; в) Нет; г) Да; д) Да; е) Да.
В первой скобке это сумма квадратов натуральных чисел, для нее известная формула есть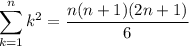 , а вторая скобка это арифметическая прогрессия с первым членом 1 и d = 1
, а вторая скобка это арифметическая прогрессия с первым членом 1 и d = 1