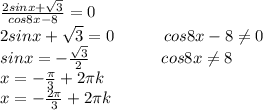Решение, а) По условию АС = AD и ВС = = BD. Отрезок АВ — общая сторона треугольников ABC и ABD (рис.75, на этом рисунке точка В лежит на луче АО; случай, когда точка В лежит на продолжении луча АО, рассматривается аналогично). Поэтому ААВС = AABD по третьему признаку равенства треугольников. Отсюда следует, что ZADB = ZACB.
6) Из равенства треугольников ABC и ABD следует также, что ZCAB = ZDAB. Это означает, что АО — биссектриса равнобедренного треугольника ACD. Следовательно, АО — также медиана треугольника ACD, т. е. DO = ОС.

1) cos5x =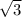 /2
/2
5x = +- П/6 +2Пk
x = +-П/30 +2Пk/5
2,3 - не поняла запись (там не всего хватает)
4)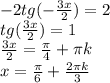
5) cosx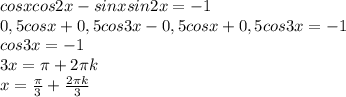
6)