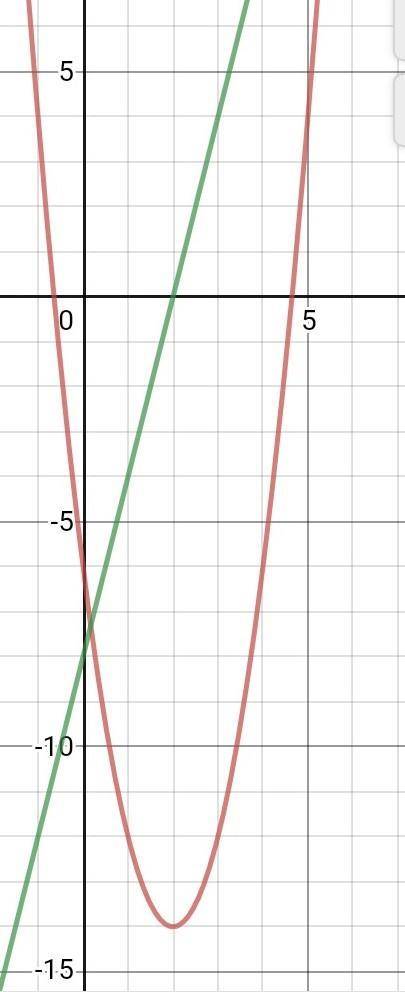
Это равнопеременные движения, их уравнения в общем виде: координаты х(t)= Xo+Vot+at²/2, графики -параболы. Скорости v(t)=Vo+at, графики -линейные. (на фото смотреть при t>0). Перемещение s=x(t)-Xo, график может быть получен смещением графика х(t)
1) для х1 имеем дано: Xo=-6м -начальная координата при t=0, Vo=-8м/с -нач. скорость, ускорение а=+4м/с² (торможение). То есть: тело сначала едет в обратную (против оси 0х) сторону, но с торможением. При t=2c останов (v=0, s=14м -максимум обратного перемещения), далее разгон в прямом направлении (v>0 и а>0). При t=4c х=-6м, т.е. тело вернулось в исходную точку, а в момент t=≈4.646c координата становится х=0 (начало координат); далее ускорение (разгон) продолжается с положительными координатами х>0 и тело уезжает в бесконечность
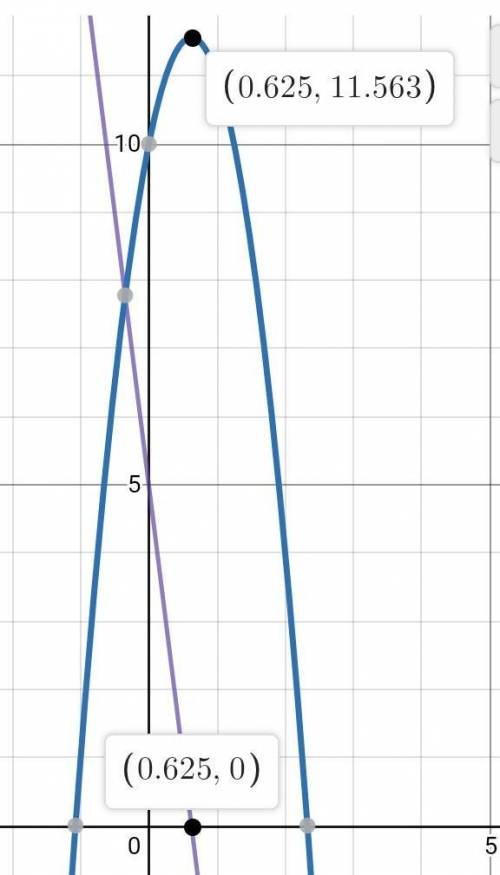
2) для х2: движение похожее, только в другую сторону. Вначале (t=0) Xo=10м, Vo=+5м/с, т.е. перемещение вдоль/по оси 0х, но тоже с торможением а=-8м/с². При t=0.625c остановка: v=0 х=11.563м максимальное. Далее перемещение в обратную, против 0х, сторону (v<0), с ускорением (и v<0, и а<0 тоже).При t=≈2.325c тело приезжает в начало координат х=0, и продолжает ускоряться с отрицательными координатами х<0
Пояснение: значения t получены решением квадратных уравнений х(t)=0 и линейных v(t)=0. Чтобы параболы хорошо прорисовать, надо взять характерные точки t=0, х=0 и х=экстремум
Δp(пуля) = p2 - p1 = m1V0/2 - m1V0 = 0,001 (75 - 150) = - 0,0075 кг*м/с
2) Зная импульс, который приобрела коробка, можем вычислить ее скорость:
p = m2 V2 => V2 = p / m2 = 0,075 / 0,05 = 1,5 м/с
3) V2 - это ее начальная скорость. Конечная, очевидно, будет равна нулю. По формуле из кинематики найдем ускорение, которое приобрела коробка:
S = - V0^2 / 2a => a = - V0^2 / 2S = - 2,25 / 0,6 = - 3,75 м/с^2
4) На коробку действует только сила трения. По второму закону Ньютона в проекции имеем:
- u mg = ma => u = - a / g = 3,75 / 10 = 0,375