Максимум
1)тело массой 11 кг скользит по наклонной плоскости с углом наклона 30°. чему равно ускорение тела, если на него действует сила трения, равная 37,3 н? ускорение свободного падения считать равным 9,8 мс2.
чему равна проекция силы тяжести на ось, которая параллельна наклонной плоскости? fтx =
н (округли до десятых).
чему равно ускорение движения тела? a =
мс2 (если необходимо, результат округли до десятых).
2)на дельтаплан действуют 4 взаимно перпендикулярные силы.
вид силы
сила тяги, fт
сила сопротивления, fс
подъёмная сила, fп
сила тяжести, fтяж
модуль силы
3287 н
3681 н
3264 н
2315 н
на рисунке показано только направление действия сил, но не отображены точные размеры векторов сил.
дельт.bmp
как изменится скорость дельтаплана в горизонтальном направлении?
скорость не изменится.
скорость уменьшится.
скорость увеличится.
как изменится высота полёта дельтаплана?
высота полёта увеличится.
высота полёта не изменится.
высота полёта уменьшится.
чему равна результирующая сила в горизонтальном направлении? fx =
н.
чему равна результирующая сила в вертикальном направлении? fy =
н.
чему равна результирующая сила, действующая на дельтаплан? fрез =
н.
все результаты округли до целого числа!
3)брусок лежит на наклонной плоскости.
его масса m = 13 кг , а угол β = 18° .
чему равна сила реакции опоры f , действующая на брусок?
g=10м/с2 .
124н
137н
130н
40н
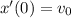 .
.
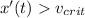 .
.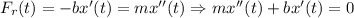
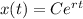 . Тогда дифференциальное уравнение имеет вид
. Тогда дифференциальное уравнение имеет вид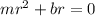
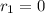
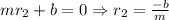
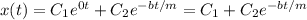
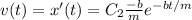
 ,
, 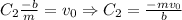 .
.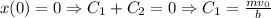
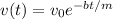
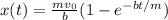
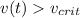 , то есть
, то есть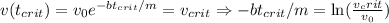
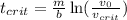
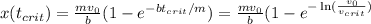
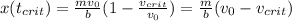
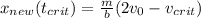
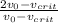 ,
,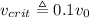 , это отношение равно
, это отношение равно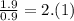 .
.
Пуля не деформируется.
Для начала введем систему отсчета: пусть начало координат лежит в месте вхождения пули в вал, а пуля движется вдоль оси X (в положительном направлении). Координату пули отметим функцией x(t). Начнем наблюдение в момент касания пулей вала. Тогда x(0) = 0. Под начальной скоростью пули понимаем скорость пули относительно начала отсчета в момент времени t=0, то есть
По аналогии с жидкостями, можно рассматривать вискозность земли, тогда сила, действующая на пулю (замедляющая сила) пропорциональна скорости пули с фактором b:
Земля проявляет вискозность только при достаточной скорости пули, допустим при
Пренебрегая силой тяжести, а значит и движением пули по вертикали, запишем второй закон Ньютона:
Пусть
Решением является линейная комбинация функций:
То есть
Тогда
Так как
Тогда
Соответственно, в любой момент времени координата пули прямо пропорциональна начальной скорости, то есть удвоение начальной скорости приведет к удвоению пройденного расстояния.
Найдем это расстояние:
Пусть момент, когда движение пули перестанет следовать законом жидкостей, означает для нас остановку пули. Тогда пуля движется до тех пор, пока
Тогда
Соответственно
При удвоении начальной скорости, конечная координата равна:
Тогда отношение нового пути к старому равно
При, допустим,