Question

Решить
с какой высоты наклонной плоскости должен скользить груз массой m, чтобы остановиться на расстоянии s от конца наклонной плоскости, если коэф.трения груза об поверхность k, а угол наклона альфа

Answer 1

$h = \frac{ s }{ ( 1/ \mu - 1/ tg{\alpha} )( \cos{\alpha} - \mu \sin{\alpha} )^2 }$  , при условии:  $arctg{(\mu)} < \alpha < arcCtg{(\mu)}$  ;

*** если же переход от наклонной плоскости скруглённый, и: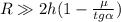  $R \gg 2h ( 1 - \frac{\mu}{tg{\alpha}} )$  , то:

$h = \frac{ s }{ 1/\mu - 1/tg{(\alpha)} }$  .

Объяснение:

По закону сохранений энергии:

$E_{ko} + E_{no} - A_\alpha = E_{k\alpha} + E_{n\alpha}$  ;

где:

$E_{ko} = 0$  и  $E_{no} = mgh$  – начальные значения кинетической и потенциальной энергии;

$E_{k\alpha} = \frac{mv_\alpha^2}{2}$  и  $E_{n\alpha} = 0$  – значения кинетической и потенциальной энергии перед ударом о горизонтальную поверхность, в самом низу наклонной плоскости;

$A_\alpha$  – работа силы трения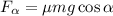 на наклонной плоскости;

$A_\alpha = F_\alpha \cdot L$  – работа

силы трения  $F_\alpha = \mu mg \cos{\alpha}$  на наклонной плоскости,

где: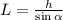  $L = \frac{h}{\sin{\alpha}}$  – длина наклонной плоскости;

$A_\alpha = \frac{ \mu mgh }{tg{\alpha}}$  ;

В итоге:

$mgh - \frac{ \mu mgh }{tg{\alpha}} = \frac{mv_\alpha^2}{2}$  ;

(*) $\frac{v_\alpha^2}{2} = gh ( 1 - \frac{\mu}{tg{\alpha}} )$  ;

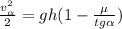Из этого вытекает очевидное условие, что:

$1 - \frac{\mu}{tg{\alpha}} 0$  ;

$1 \frac{\mu}{tg{\alpha}}$  ;

$tg{\alpha} \mu$  , т.е. угол наклона должен быть более значения:  $\alpha arctg{(\mu)}$  , иначе груз вообще не сдвинется с места, и, разумеется, никакого расстояния  $s$  не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты  $h$  .

Теперь «удар», т.е. переход с наклонной плоскости на горизонталь. Во время удара теряется вертикальная составляющая импульса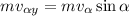  $mv_{\alpha y} = mv_\alpha \sin{\alpha}$  . Это происходит почти мгновенно (  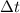$\Delta t$  ), под воздействием гасящей его чрезвычайно резко возрастающей на время гашения силы реакции опоры (и веса – соответственно)  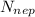$N_{nep}$  . Удар груза об опору в момент его перехода на горизонталь будем считать абсолютно неупругим, происходящим таким образом, что груз после него не подскакивает. Тогда можно записать, что:

$mv_{\alpha y} - N_{nep} \Delta t = 0$  ;

$N_{nep} = \frac{mv_{\alpha y}}{\Delta t}$  ;

За это время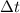  $\Delta t$  груз так же заметно замедляется под воздействием чрезвычайно резко возрастающей на время гашения силы трения:

$F_{nep} = \mu N_{nep} = \mu \cdot \frac{mv_{\alpha y}}{\Delta t}$  ;

Соответственно, гасится и горизонтальный импульс:

$mv_\alpha' = mv_{\alpha x} - F_{nep} \Delta t = mv_\alpha \cos{\alpha} - \mu \cdot \frac{mv_{\alpha y}}{\Delta t} \cdot \Delta t =$

$= mv_\alpha \cos{\alpha} - \mu mv_\alpha \sin{\alpha} = mv_\alpha ( \cos{\alpha} - \mu \sin{\alpha} )$  ;

$v_\alpha' = v_\alpha ( \cos{\alpha} - \mu \sin{\alpha} )$  ;

Из последнего вытекает очевидное условие, что:

$\cos{\alpha} - \mu \sin{\alpha} 0$  ;

$\cos{\alpha} \mu \sin{\alpha}$  ;

$\frac{\cos{\alpha}}{\sin{\alpha}} \mu$  ;

$tg{\alpha} < \frac{1}{\mu}$  , т.е. угол наклона должен быть не более определённого значения:  $\alpha < arctg\frac{1}{\mu} = arcCtg{(\mu)}$  , иначе груз после удара о горизонтальную плоскость просто остановится, и никакого расстояния  $s$  не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты  $h$  .

Кинетическая энергия груза после «ударного» торможения:

$E_{k\alpha}' = \frac{1}{2} mv_\alpha'^2 = \frac{1}{2} mv_\alpha^2 ( \cos{\alpha} - \mu \sin{\alpha} )^2$  ;

Далее, снова по закону сохранений энергии (с учётом неизменного значения потенциальной):

$E_{k\alpha}' - A_{ocm} = E_{k}'$  ;

где:

$A_{ocm} = F_{mp} \cdot s = \mu mg s$  – работа силы трения на горизонтальном участке до остановки;

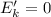а  $E_{k}' = 0$  – конечная кинетическая энергия (остановка);

$\frac{1}{2} mv_\alpha^2 ( \cos{\alpha} - \mu \sin{\alpha} )^2 = \mu mg s$  ;

$\frac{v_\alpha^2}{2} = \frac{ \mu g s }{ ( \cos{\alpha} - \mu \sin{\alpha} )^2 }$  ;

Учитывая (*):

$gh ( 1 - \frac{\mu}{tg{\alpha}} ) = \frac{ \mu g s }{ ( \cos{\alpha} - \mu \sin{\alpha} )^2 }$  ;

$h ( 1 - \frac{\mu}{tg{\alpha}} ) = \frac{ \mu s }{ ( \cos{\alpha} - \mu \sin{\alpha} )^2 }$  ;

$h = \frac{ s }{ ( 1/ \mu - 1/ tg{\alpha} )( \cos{\alpha} - \mu \sin{\alpha} )^2 }$  .

*** Если же переход от наклонной плоскости гладкий, и при этом: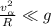 $\frac{v_\alpha^2}{R} \ll g$  , т.е. радиус перехода:  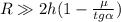$R \gg 2h ( 1 - \frac{\mu}{tg{\alpha}} )$  , то «ударная» потеря – пренебрежима, и:  $v_\alpha' = v_\alpha$  , а, значит:

$h = \frac{ \mu s }{ 1 - \mu Ctg{(\alpha)} } = \frac{ s }{ 1/\mu - 1/tg{(\alpha)} }$  .