1 . 3 , 2 / 5
9 5
Третий закон Кеплера гласит - квадраты периодов обращения планет вокруг Солнца относятся , как кубы больших полуосей орбит планет .
Проверим закон Кеплера на планете Земля .
Принято , что расстояние от планета Земля до планеты Солнце равно 1 астрономическая единица ( а . е . ) и также считают,, что Солнце - центр нашей планетарной системы,, следовательно оно относительно нас недвижимо и формула (Тз/Тс)² = (Аз/Ас)³ превращается в формулу (Тз/1)²=(Аз/1)³⇒ (Тз)² = (Аз)³⇒Тз = √(Аз)³ .
Так как на планете Земля Аз ( период вращения вокруг планеты Солнце ) 1 а . е .⇒ Тз = √1³ = 1 , то есть ≈ 365 земных дней .
Теперь можно вычислить " звёздный период вращения планеты Марс " вокруг планеты Солнце :
Тм = √(1,5)³ ≈ 1,837 земного года ≈ 1,837*365 ≈ 671 земной день .
2 . По формуле КПД = Qп / Qз . ( Qп-полезное количество теплоты на нагревание печи ) , Qз-затраченное количество теплоты от сгорания угля ) .
Qп = c*m1*( t2 - t1 ) . ( c-удельная теплоемкость кирпича , m1-масса печи = 1200кг , t1-начальная температура печи , t2 - конечная температура печи ) .
Qз = q*m2 . ( q - удельная теплота сгорания угля , m2 - его масса КПД = 0,3 ) . Подставим :
КПД=c*m1*(t2 - t1) / q*m2. выразим m2.
m2 = c*m1*( t2 - t1 ) / q*КПД .
m2 = 750*1200*( 50 - 10 ) / 30*10^6*0,3 = 4кг .
Объяснение:
Прости , если не правильно ♥
Задание 5
Разделим всё движение на два этапа как и описано в условии и опишем эти этапы.
Первый этап ("Мотоциклист проехал 30 км за 20 мин")
S1 = 30км
t1 = 20 мин = 1/3 часа
v1 = 30км / (1/3) часа = 90 км/ч
Второй этап ("а затем ехал со скоростью 70 км/ч в течение 1 ч 40 мин")
v2 = 70км/ч
t2 = 1ч 40мин = 1 +2/3 часа = 5/3 часа
S2 = 70км/ч * (5/3) часа = 350/3 км/ч
Средняя скорость на всём пути будет весь путь поделить на всё время.
Vсреднее = (S1+S2)/(t1+t2) = (30 км + 350/3 км) / (1/3 ч + 5/3 ч) = (440/3) / (6/3) = 440/6 =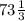 км/ч
км/ч
Задание 6.
V = 72 км/ч = 72 000 м / 3600 сек = 20 м/сек
t = 40 сек
a = v / t = 20 м/сек / 40 сек = 0,5 м/сек²
Задание 7.
Потому что вещество (воздух) состоит не только из молекул, но и из расстояния между ними.
Объяснение: