Дано: l1 = 16см ; l2 = 25см (l - длина)
Найти: T(период колебаний пружинного маятника) - ?
У нас дано две длины l1 - не деформированная, то есть не растянутая, а l2 уже растянутая. Найдём разность этих длин и получим l2-l1=25 - 16 = 9 (см) - это мы нашли удлинение пружины, то есть общее удлинение.
Чтоб рассчитать Период колебаний пружинного маятника, мы вспомним, что период колебаний бывает пружинного и нитяного маятников, нам из этого, нужен пружинный, следовательно находим формулу периода колебаний пружинного маятника: T= 2π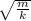
. Нам неизвестна масса (m), за-то известно удлинение пружины.
Вспомним закон Гука: Fупр = k|x|, от сюда выразим удлинение k=F/|x| => От сюда мы можем заменить F = mg (Сила тяжести), следует k=mg/|x|, теперь вернёмся к формуле пружинного маятника T= 2π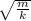, подставляем и получаем => T= 2π
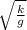= 2*3,14*3/√10=5.961 округляем до целого и получаем 6(секунд).
ответ: T = 6 секунд
Считаем вторую площадь: S2=(a/2)*(a/2)=0,000625 м^2
Площадь уменьшилась в S1/S2=0,0025/0,000625=4 раза
P=F/S
P=mg/S
Найдем, во сколько раз уменьшилась масса:
Изначальная масса m1=p*V1 (где p - плотность тела)
m1=p*a^3=0,000125p
Конечная масса m2=p*V2
m2=p*(a/2)^3=0,000015625p
Считаем во сколько уменьшилась масса: m1/m2 =8 раз
m1=8m2
S1=4S2
Отношение давлений:
P1/P2=m1g/S1 : m2g/S2 = m1*g*S2/ S1*m2*g = 8m2*g*S2 / 4S2*m2*g = 8/4=2
Тогда P1=2*P2, а значит давление увеличится в 2 раза