1. Сила Амера, действующая на проводник: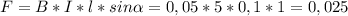 
ньютон. При перемещении проводника сила Ампера совершит работу: 
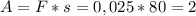джоуля.
ответ: 2 Дж.
2. Сила Лоренца, действующая на электрон со стороны магнитного поля, придаёт ему центростремительное ускорение. Приравняем силу Лоренца к произведению массы электрона на его центростремительное ускорение: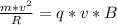 
. Сократим скорость: 
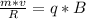. Так как произведение m*v=p (произведение массы на скорость равно импульсу), то индукция равна: 
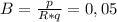тесла.
ответ: 0,05 Тл.
3. Так как линии магнитной индукции направлены параллельно направлению тока, то на проводник сила Ампера не действует.
ответ: 2) Не изменится.
Раз бросают под углом α = 30°, то сразу находим путь(гипотенузу).
h₂ = h₁*cos 30° = 40 м . Теперь находим конечную скорость в отсутствие внешних сил, то есть в безвоздушном пространстве: V₂ = √(2gh₂) = √(2*10*40)+10 м/с. = 10 + √800 м/с. Но у нас есть одна помеха - сопротивление воздуха. А значит, мы можем найти кинетическую энергию:
E₁ = m(V₁+V₀)²/2 = 1 кг*(12м/с+10м/с)²/2 = 242 Дж.
Энергия без затрат(то есть со скоростью в самом конце = 10м/с + √800 м/с) равна m(V₂+V₀)²/2 = 1 кг*(10 м/с + √800 м/с)/2 = 732,8427 Дж.
Видна большая разница между E₁ и E₂ - это и есть работа сопротивления воздуха. Она равна 490,8427 Дж
ответ:Система отсчета – это совокупность тела отсчета и системы пространственных координат, жестко связанной с телом отсчета и снабженной часами.
Материальная точка (частица) – это тело, размерами которого в условиях данной задачи можно пренебречь. Одно и то же тело в различных условиях или может считаться материальной точкой, или нет.
Кинематический закон движения – это функция, выражающая положение точки в любой момент времени: r = r(t) (2.1)
Уравнение (2.1) является векторной формой закона. Движение материальной точки полностью определено, если координаты материальной точки заданы в зависимости от времени: x = x(t), y = y(t), z = z(t) . (2.2)
Траектория – это кривая, которую описывает радиус-вектор r(t) координат материальной точки (или тела) с течением времени.
Вектор перемещения ∆r = r - r0 – это вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиус-вектора точки за рассматриваемый промежуток времени):
∆r = r - r0 = r(t) - r(t0) . В пределе ∆t→0 модуль элементарного перемещения равен элементарному пути: |dr| = ds .
Объяснение: