Имеем: g = 1,6 м/c²; T = 4,9 c. Найти: L - ?
1. Формула периода математического маятника: 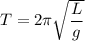 .
.
2. Выразим длину: 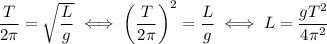 .
.
3. Численно получим: 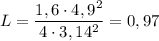 (м).
(м).
Дано: C = 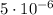 Ф; T = 0,001 c. Найти: L - ?
Ф; T = 0,001 c. Найти: L - ?
1. Формула Томсона: 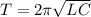 .
.
2. Индуктивность из (1): 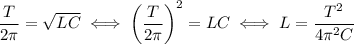 .
.
3. Численно получим: 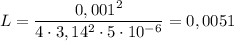 (Гн).
(Гн).
4. Перевод: 0,0051 Гн = 5,1 мГн.
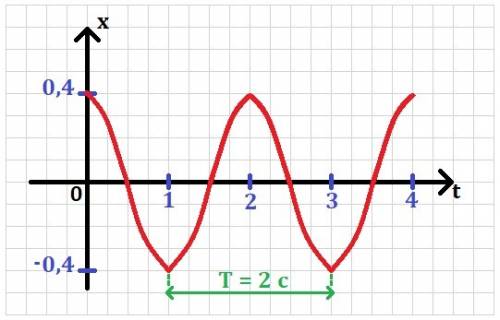
ответ: 5,1 мГн.======================Задача #3Имеем: x = 0,4cos(πt). Найти: A, T - ? Построить: x(t).
1. Уравнение гармонических колебаний в общем виде: 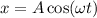 , отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
, отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
2. Формула циклической частоты: 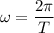 , значит период:
, значит период: 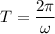 .
.
3. Численно: 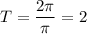 (c).
(c).
График зависимости x(t) смотри в приложении.
1 в
Объяснение:
Температура однородного медного цилиндрического проводника длинной 10м в течении 57 с повысилась на 10К. Определить напряжение, которое было приложено к проводнику в это время. Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь
L=10 м
t=57 c
∆T= 10 K
U- ?
РЕШЕНИЕ
Количество тепла выделенное проводником по з-ну Дж-Ленца
Q1=U^2/R *t (1)
Сопротивление проводника длиной L
R=λL/S (2)
λ-удельное электрическое сопротивление меди =0.017 Ом*мм2/м=0.017*10^-6 Ом*м
S –поперечное сечение проводника
L-длина проводника
Подставим (2) в (1)
Q1=U^2/( λL/S) *t = U^2*S*t/( λL) (3)
Количество тепла полученное проводником от работы тока
Q2=сm∆T=cVp∆T=cLSp∆T (4)
С-удельная теплоемкость меди =400 Дж/кг*К
m-масса проводника
V-объем проводника
р-плотность меди =8920 кг/м3
по условию задачи потерь тепла нет, тогда
Q1=Q2
Приравняем (3) и (4)
U^2*S*t/( λL)= cLSp∆
U^2 =1/t *( cLp∆T)*( λL)=1/t *c λ p L^2*∆T
U=√(1/t *c λ p L^2*∆T)= √(1/57*400*0.017*10^-6*8920*10^2*10) = 1 В
ответ напряжение 1 В