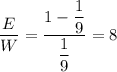На высоту 5 м подъёмный кран поднимает 4 м3 цементного раствора, плотность которого равна 2036 кгм3, (g=10 мс2).

Какую работу совершает подъёмный кран?

ответ: подъёмный кран совершает работу, равную ?
Дж. ФАСТОМ РЕШИТЕ

👇

Увидеть ответ

Открыть все ответы

Ответ:

andrejpyankoff

17.09.2020

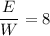
ответ: $\dfrac{E}{W} = 8$

Объяснение:

Запишем уравнение гармонических колебаний в общем виде:

$x(t) = A \sin ( \omega t + \phi_{0})$

Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.

Отсюда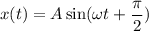 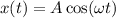$x(t) = A \sin ( \omega t +\dfrac{\pi }{2} )$ ⇒ $x(t) = A \cos ( \omega t)$ (1)

Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.

То-есть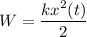 $W=\dfrac{kx^{2}(t) }{2}$ , но согласно уравнению (1) получим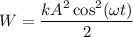 $W=\dfrac{kA^{2} \cos^{2} ( \omega t)}{2}\\$

Аналогично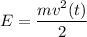 $E = \dfrac{mv^{2}(t) }{2}$ , однако мы знаем, что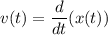 $v(t) =\dfrac{d}{dt} (x(t))$

Тогда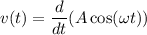 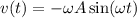$v(t) =\dfrac{d}{dt} ( A \cos ( \omega t))$ ⇒ $v(t) =-\omega A \sin( \omega t)$ , а это значит что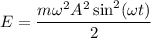 $E = \dfrac{m\omega^{2} A^{2} \sin^{2} ( \omega t)}{2}$

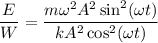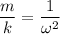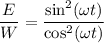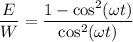Поэтому $\dfrac{E}{W} = \dfrac{m\omega^{2} A^{2} \sin^{2} ( \omega t)}{kA^{2} \cos^{2} ( \omega t)}\\}$ , так как $\dfrac{m}{k} = \dfrac{1}{\omega^{2} }$ , то $\dfrac{E}{W} = \dfrac{\sin^{2} ( \omega t)}{\cos^{2} ( \omega t)}\\}$ ⇒ $\dfrac{E}{W} = \dfrac{1 - \cos^{2} ( \omega t)}{\cos^{2} ( \omega t)}\\}$ (2)

Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1)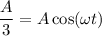 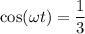$\dfrac{A}{3} = A \cos ( \omega t)$ ⇒ $\cos ( \omega t) = \dfrac{1}{3}$ , следовательно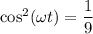 $\cos^{2} ( \omega t) = \dfrac{1}{9}$

Возвращаясь к уравнению (2) получим $\dfrac{E}{W} = \dfrac{1 - \dfrac{1}{9} }{\dfrac{1}{9} }} = 8$

4,8(48 оценок)

Ответ:

nogood2

17.09.2020

ответ: 300 000 Н (300 кН)

Объяснение:

Выталкивающая сила (сила Архимеда) определяется по формуле F=P*g*V, где Р — плотность жидкости (обычно обозначается греческой буквой «ро»), g — ускорение свободного падения, V — объём тела.

Плотность воды можно найти в специальной таблице, она равна 1000 кг/м³. Ускорение свободного падения тоже известно, g≈10 м/с² (иногда берут более точное значение — 9,8 м/с², зависит от условия задачи). Объём тела (мяча) по условию равен 30 м³. Подставив эти значения в формулу, получим:

F= 1000 (кг/м³)*10 (м/с²)*30(м³) = 300 000 Н = 300 кН.

ответ: 300 кН

4,4(4 оценок)

Это интересно:

01.10.2020

Как встречаться с парнем из другой школы: советы и техники...

Здоровье

06.07.2021

Как повысить либидо: простые способы улучшения сексуальной жизни...

Компьютеры-и-электроника

28.05.2023

Как зарабатывать в игре RuneScape не имея членства: лучшие способы...