Цикл Карно – це цикл ідеальної теплової машини. В ній відсутні втрати на теплопровідність, теплове випромінювання, тертя і т.п.
Цикл Карно встановлює основні співвідношення процесу переходу теплоти від одного тіла до іншого з перетворенням цієї теплоти.
Розглянемо коловий процес, в результаті якого тепло, відняте від якогось тіла, можна перетворити в роботу і притому якнайкраще.
Карно довів теорему: із всіх періодично діючих теплових машин, що мають однакові температури нагрівачів і холодильників, найбільший ККД мають оборотні машини: при цьому ККД оборотних машин, що працюють при однакових температурах нагрівачів і холодильників, дорівнюють один одному і не залежать від конструкції машини.
Цикл Карно складається з двох ізотерм і двох адіабат .
ІПрямоугольник 3882зотермічне розширення і стиск задані, відповідно, кривими 1-2 і 3-4, адіабатне розширення і стиск-, відповідно, кривими 2-3 і 4-1. Для виконання циклу Карно необхідні термостат з температурою Т1 (нагрівник) і термостат з температурою Т2 (холодильник), причому Т1>Т2. При проходженні адіабатних ділянок циклу система повинна бути термоізольованою від навколишнього середовища.
Визначимо ККД циклу Карно. При ізотермічному процесі U=0 і робота розширення газу А12 дорівнює кількості теплоти Q1, що отримав газ від нагрівника:
При адіабатному розширенні робота виконується за рахунок зміни внутрішньої енергії:
При ізотермічному стисканні газу виконується робота А34 і газ віддає холодильнику кількість теплоти Q2
робота
А = А12 + А23 + А34 + А41 = Q1 + A23 - Q2 - A23 = Q1 - Q2.
Термічний ККД циклу Карно
Використаємо рівняння адіабат 2-3 і 4-1:
з верху фото

Закон прямолинейного распространения света: свет в оптически однородной среде
распространяется прямолинейно.
Доказательством этого закона является наличие тени с резкими границами от
непрозрачных предметов при освещении их точечными источниками света (источники,
размеры которых значительно меньше освещаемого предмета и расстояния до него). Тщательные эксперименты показали, однако, что этот закон нарушается, если свет
проходит сквозь очень малые отверстия, причем отклонение от прямолинейности
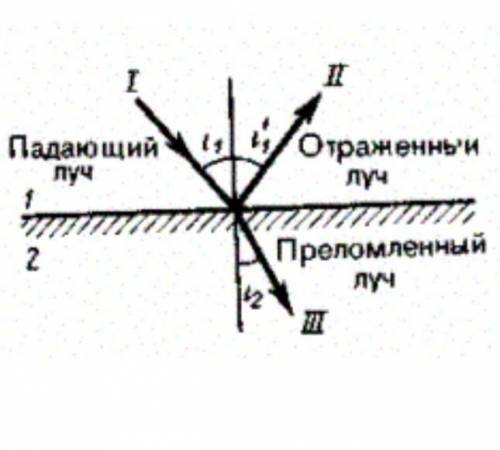
распространения тем больше, чем меньше отверстия. Закон независимости световых пучков: эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. Разбивая световой поток на отдельные световые пучки (например, с диафрагм), можно показать, что действие выделенных световых пучков независимо. Закон отражения света. Закон преломления света. Если свет падает на границу раздела двух сред (двух прозрачных веществ), то падающий луч I разделяется на два отраженный II и преломленный III,
направления которых задаются законами отражения и преломления. Закон отражения: отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред точке падения; угол i'1, Закон преломления: луч падающий, луч преломленный и перпендикуляр,проведенный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:где n21 — относительный показатель преломления второй среды относительно первой. Этот закон еще называют законом Снеллиуса. Индексы в обозначениях углов i1, i′1, i2 указывают, в какой среде (первой или второй) вдет луч. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления: Абсолютным показателем преломления среды называется величина n, равная отношению скорости с электромагнитных волн в вакууме к их фазовой скорости v вcреде: Сравнение с формулой дает, что n = εµ , где ε и µ — соответственно электрическая и магнитная
проницаемости среды. Учитывая (2), закон преломления (1) можно записать в виде
Полное внутреннее отражение
Относительный показатель преломления двух сред равен отношению их абсолютных
показателей преломления:
Тогда закон преломления можно записать в виде. Из симметрии выражения вытекает обратимость световых лучей. Если обратить
луч III, заставив его падать на границу раздела под углом i2, то преломленный
луч в первой среде будет распространяться под углом i1 т. е. пойдет в обратном направлении вдоль луча I. Если свет распространяется из среды с большим показателем преломления n1
(оптически более плотной) в среду с меньшим показателем преломления n2 (оптически
менее плотную) (n1 > n2), например из стекла в воду, то, согласно. Отсюда следует, что преломленный луч удаляется от нормали и угол преломления i2 больше, чем угол падения i1 (рис. 2, а). С увеличением угла падения увеличивается угол преломления (рис. 2, б, в) до тех пор, пока при некотором угле падения (i1 = iпр,) угол преломления не окажется равным π/2. Угол iпр называется предельным углом. При углах падения i1 > iпр весь падающий свет полностью отражается (рис. 2, г). По мере приближения утла падения к предельному интенсивность преломленного луча уменьшается, а отраженного — растет (рис. 2, а—в). Если i1 = iпр, то интенсивностьпреломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 2, г). Таким образом, при углах падения в пределах от iпр, до π/2 луч не преломляется, а полностью отражается в первую среду, причём интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.
Предельный угол iпр определим из формулы при подстановке в нее i2 = π/2.
Уравнение (2) удовлетворяет значениям угла iпр при n2 ≤ n1. Следовательно, явление
полного отражения имеет место только при падении света из среды оптически более
плотной в среду оптически менее плотную.
Явление полного отражения используется в призмах полного отражения. Показатель
преломления стекла равен n ≈ 1,5, поэтому предельный угол для границы стекло —
воздух равен iпр =arcsin(l/l,5) = 42°. Поэтому при падении света на границу стекло —
воздух при i > 42° всегда будет иметь место полное отражение. На рис. 3, а—в
показаны призмы полного отражения, позволяющие: а) повернуть луч на 90°; б)
повернуть изображение; в) обернуть лучи. Такие призмы применяются в оптических
приборах (например, в биноклях, перископах).
Дано: d=30 см, φ0=5400 В, l=15 см, φ1−?
Потенциал φ0 на поверхности сферы (то есть в точке
A) радиусом r, имеющей некоторый заряд q, определим по формуле:
φ0=kqr
Так как радиус сферы равен половине диаметра (r=d2), то имеем:
φ0=2kqd(1)
Потенциал φ1 на расстоянии l от поверхности сферы (в точке B) можно найти из формулы:
φ1=kqr+l
Учитывая, что r=d2, получим:
φ1=kqd2+l
Домножим и числитель, и знаменатель на 2:
φ1=2kqd+2l(2)
Теперь поделим (2) на (1):
φ1φ0=dd+2l
В итоге получим такое решение:
φ1=φ0dd+2l
Посчитаем численный ответ:
φ1=5400⋅0,30,3+2⋅0,15=2700В
ответ:2700В