Дано:
m1 = 200 кг
m2 = 50 кг
v1 = 2 м/с
v2 = 1,2 м/с
Найти:
u = ?
delta p = ?
Сохраняется импульс системы p, что является ответом на вопрос в пункте а).
б) Тележка движется горизонтально, а мешок с песком - вертикально. Поэтому выберем горизонтальную ось, т.к. вдоль неё сохраняется движение тел. Кроме того, удар мешка с тележкой является неупругим, то есть после столкновения тела движутся с одинаковой скоростью. Тогда закон сохранения импульса будет:
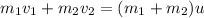
Горизонтальная составляющая скорости мешка равна нулю (т.к. мешок падает строго вертикально), а тележка пусть движется вдоль оси Х (импульс будет со знаком "плюс"), поэтому:
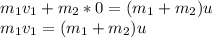
Остаётся выразить скорость u и найти её:
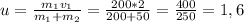
1,6 м/с - скорость тележки с мешком песка.
в) Найдём проекции импульсов. Направим оси так, что до своего падения мешок двигался против оси Y (импульс будет со знаком "минус"), а после - всё так же сонаправленно оси Х. Тогда:
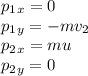
Теперь найдём проекции изменения импульса:
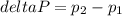
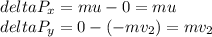
И теперь само изменение импульса:
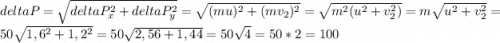 Модуль изменения импульса имеет то же значение, что и само изменение: 100 кг · м/с.
Модуль изменения импульса имеет то же значение, что и само изменение: 100 кг · м/с.
ответ: а) сохраняется импульс p, б) 1,6 м/с в) 100 кг · м/с.
Возьмем СИСТЕМУ ОТСЧЕТА относительно Земли.
Дано:
M = 300 г = 0,3 кг
m = 100 г = 0,01 кг
u = 100 м/c
v = ?
1) состояние - это покой ракеты и газов.
2) Состояние - вырывающиеся газы из сопла и летящая ракета.
За малый промежуток времени значительное изменение импульса не произойдет, значит воспользуемся ЗАКОНОМ СОХРАНЕНИЯ ИМПУЛЬСА:
(Без векторов, ось координат направлена вдоль движения ракеты вверх)
0 = Mv - mu (газы вырываются мгновенно, значит их нет в массе взлетающей оболочки)
Mv = mu
v = (m/M) * u = (0,1 / 0,3) * 100 = (1/3) * 100 = 33,33 м/c - модели ракеты.
ответ: скорость модели ракеты равна 33,3 м/c.
L =0,4Гн
С =90пФ = 9*10^-11 Ф
Т = 2pi *sqrt(LC)
2.
lambda = 2 cm= 2*10^-2 м
(lambda) = с/v
v = c / (lyambda)