Скорость сближения мыши и кота:
v = v₁ - v₂ = 5,2 - 1,5 = 3,7 (м/с)
Время, необходимое коту для того, чтобы догнать мышь:
t₁ = S/v = 9 : 3,7 ≈ 2,43 (c)
Время, необходимое мыши для того, чтобы успеть забежать в нору:
t₂ = S₂/v₂ = 4 : 1,5 = 2 2/3 ≈ 2,67 (с)
Так как t₂ > t₁, то кот успеет догнать мышь прежде, чем она успеет забежать в нору.
Расстояние, которого не хватит мыши:
S₂' = v₂*(t₂ - t₁) = 1,5 * 0,24 = 36 (см)
ответ: кот догонит мышь на расстоянии 36 см от норы.
300м
Объяснение:
Граф. метод։
У нас на графике трапеция. Перемещение в данном случае равна площади под графиком(Если б скорость уходила бы в минус, тогда для рассчётов вектора перемещения нам понадобилось бы вычесть площадь минусовой части V). Площадь трапеции равна полусумме его оснований умноженное на её высоту.
⇒|S(вектор перемещения)| =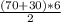 = 300м
= 300м
Анал. метод։
0) V₀ = 0м/c, V₁ = 6м/c, Δt = 30с
⇒ a₀ = (V₁-V₀)/Δt = 0.2м/c²
⇒ S₀ = a₀Δt²/2 = 90м
1) a₁ = 0м/c²
⇒ S₁ = V₁ × t₁ = 6 × 30 = 180м
2) V₁ = 6м/c V₂ = 0 Δt = 10с
⇒ a₂ = -0.6м/c²
⇒ S₂ = V₁×Δt + a₂Δt²/2 = V₁²/(2×a₂) = 30м
⇒ ∑S = 90 + 180 + 30 = 300м