Цирковой акробат массой 90 кг, бегущий со скоростью 4,9 м/с, догоняет лошадь массой 215 кг, движущуюся со скоростью 2,4 м/с, и вскакивет на неё. Определи скорость лошади в тот момент, когда акробат вскочил на неё.
Пусть масса акробата — m1, скорость акробата — v1, масса и скорость лошади — m2 и v2 соответственно. p1 — импульс акробата до вскакивания на лошадь, p1’ — после, p2 и р2’ — импульс лошади до и после вскакивания на неё акробата соответственно.
По закону сохранения импульса:
р1 + р2 = р1’ + р2’
Так как акробат вскочил на лошадь, импульс у них после вскакивания будет общим (назовём его р’):
р1 + р2 = р’
Импульс рассчитывается по формуле р = m*v, где m — масса, v — скорость. Тогда закон сохранения импульса для данной задачи можно записать как
m1v1 + m2v2 = v’(m1 + m2)
Здесь v’ — искомая скорость акробата на лошади;
p’ = v’(m1 + m2): массы складываются, так как акробата и лошадь теперь можно рассматривать как одно «тело», скорость которого мы ищем (мы ищем скорость лошади после прыжка акробата, а значит, скорость лошади, на которой сидит акробат).
1) 20 л = 0,02 м^3. Плотность воды 1000 кг/м^3. Масса=плотность*объем=20 кг. Сила тяжести= 10*20 (ускорение свободного падения*масса)=200 Н. (нарисуй стакан воды, рядом подпиши Fтяж. со стрелкой вниз, поскольку сила тяжести всегда направлена вниз, если можешь сам) 2) Если мы знаем силу тяжести и не знаем массу, то надо силу разделить на у.с.п., т.е. 19,6/9,8=2 кг. 3) Сила тяжести, действующая на человека на Луне, в 6 раз меньше, чем на Земле. 4) В четвертом могу только сказать, что надо из данных массы и объема найти плотность шара и сравнить его с плотностью меди (если р шара<р меди, то он имеет полость)
В каждом случае нужно помнить, что луч падающий и луч отраженный в случае с плоским зеркалом равны. 1) α=β γ=2(α+β) - по условию задачи γ=4α α=γ/4
2) чтобы луч стал отклоняться на 50 ° от своего начального положения ( когда луч шел перпендикулярно зеркалу), то его надо запустить под углом 25° (угол падения 25°, угол отражения 25°, итого разница составит 50°). Чтобы угол падения стал 25° на такой угол нужно повернуть зеркало.
3) между лучом и перпендикуляром, по которому должен отразиться этот луч, угол 40°. Значит на угол падения придется 20°. Значит зеркало нужно расположить под углом в 20° к горизонту, чтобы падающие лучи отражались вертикально.
ответ: 3,1 м/с
Объяснение:
Пусть масса акробата — m1, скорость акробата — v1, масса и скорость лошади — m2 и v2 соответственно. p1 — импульс акробата до вскакивания на лошадь, p1’ — после, p2 и р2’ — импульс лошади до и после вскакивания на неё акробата соответственно.
По закону сохранения импульса:
р1 + р2 = р1’ + р2’
Так как акробат вскочил на лошадь, импульс у них после вскакивания будет общим (назовём его р’):
р1 + р2 = р’
Импульс рассчитывается по формуле р = m*v, где m — масса, v — скорость. Тогда закон сохранения импульса для данной задачи можно записать как
m1v1 + m2v2 = v’(m1 + m2)
Здесь v’ — искомая скорость акробата на лошади;
p’ = v’(m1 + m2): массы складываются, так как акробата и лошадь теперь можно рассматривать как одно «тело», скорость которого мы ищем (мы ищем скорость лошади после прыжка акробата, а значит, скорость лошади, на которой сидит акробат).
Итак, m1v1 + m2v2 = v’(m1 + m2). Выразим отсюда v’ :
v’ =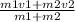
Подставим значения из условия:
v’ =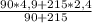 ≈ 3,1 м/с
≈ 3,1 м/с