Объяснение:
При сгорании каменного угля выделяется количество теплоты Q1=q*m1, где q — удельная теплота сгорания каменного угля (=29,3*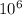
Дж/кг), m1 — искомая масса каменного угля.
Для нагревания чугуна нужно количество теплоты Q2=c*m2*(T2 - T1), где с — удельная теплоёмкость чугуна (=500 Дж/кг), m2 — масса чугуна, T2 — конечная температура чугуна, Т1 — начальная температура чугуна.
То, что КПД печи равен 20%, значит, что только 20% теплоты, выделившейся при сгорании угля, идёт на нагревание чугуна:
Q2=0,2*Q1, или
c*m2*(T2 - T1) = 0,2*q*m1
Выразим из этой формулы m1:
m1=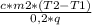 
Подставим значения из условия:
m1 = (500 Дж/кг*°С * 10 000 кг * (1010°С - 10°С)) / (0,2 * 29,3*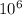 Дж/кг) =
(500 Дж/кг*С *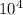 
кг * 10³С)/(0,2 * 29,3* 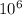Дж/кг) = 5000 Дж/5,86 Дж/кг ≈
853,2 кг.
ответ: 853,2 кг.
2. Проводники и диэлектрики в электрическом поле. Конденсаторы.
Напряженность электрического поля у поверхности проводника в вакууме:
0
En
ε
σ
=== ,
где σ – поверхностная плотность зарядов на проводнике, напряженность поля направлена
по нормали к поверхности проводника.
Энергия заряженного проводника:
W === qϕ ,
где q – заряд проводника, φ – потенциал проводника.
В однородном изотропном диэлектрике, заполняющем все пространство:
ε
E0
E
r
r
=== ,
где E0
r
– поле, созданное той же системой зарядов в вакууме, ε – диэлектрическая
проницаемость диэлектрика.
Вектор D
r
электрического смещения:
D 0E P
r r r
=== ε +++ ,
где P
r
- вектор поляризации. Для изотропных диэлектриков:
P 0E
r r
=== χε , D 0E
r r
=== εε , χ === ε +++ 1 ,
где χ – диэлектрическая восприимчивость.
Поток вектора поляризации P
r
:
∫∫∫
SdP === −−−q′′′
r r
,
где интегрирование ведется по произвольной замкнутой поверхности, q′′′- алгебраическая
сумма связанных зарядов внутри этой поверхности.
Теорема Гаусса для диэлектриков:
∫∫∫
SdD === q
r r
,
где интегрирование ведется по произвольной замкнутой поверхности, q - алгебраическая
сумма сторонних зарядов внутри этой поверхности.
Условия на границе двух диэлектриков для нормальных и тангенциальных
компонент векторов E,D,P
r r r
:
−−− === −−−σ ′′′ P n2 P n1
, D n2 −−− D n1 === σ , E2τ === E1τ
,
где σ ′′′ и σ - поверхностные плотности связанных и сторонних зарядов, вектор нормали
направлен из среды 1 в среду 2.
Емкость уединенного проводника:
ϕ
q
С = ,
где ϕ - потенциал проводника, q – заряд проводника...)